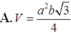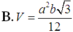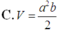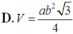Đáp án C
V = 3a.4 a 2 = 12 a 3 . Do vậy chọn đáp án C
Đáp án C
V = 3a.4 a 2 = 12 a 3 . Do vậy chọn đáp án C
Cho lăng trụ đứng ABC.A’B’C’ với đáy ABC là tam giác vuông cân tại A. Biết AB=3a góc giữa đường thẳng A’B và mặt đáy lăng trụ bằng 30 o Tính thể tích V của khối chóp A’.ABC.
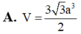
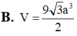
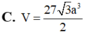
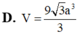
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn D C ⇀ = - 2 D B ⇀ . Góc giữa đường thẳng AC’ và mặt phẳng (A'B'C') bằng 45 0 . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
A . 9 a 3 21 4
B . 3 a 3 21 4
C . 27 a 3 21 4
D . a 3 21 4
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, góc giữa đường thẳng AC' và mặt phẳng đáy bằng 60 0 . Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
A . 3 a 3 4
B . a 3 12
C . 3 a 3 4
D . a 3 4
Cho lăng trụ đứng tam giác MNP. M’N’P’ có đáy MNP là tam giác đều cạnh a, đường chéo MP’ tạo với mặt phẳng đáy một góc bằng 60 0 .Tính theo a thể tích của khối lăng trụ MNP. M’N’P’
A. 3 a 3 2
B. 2 a 3 3
C. 3 4 a 3
D. 2 a 3 4
Cho khối lăng trụ tam giác ABC.A’B’C’ có cạnh đáy bằng 2, diện tích tam giác A’BC bằng 3. Tính thể tích khối lăng trụ
A. 2 5 3
B. 2 5
C. 2
D. 3 2
Lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 4 và diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ đó
A . 8 3
B . 6 3
C . 4 3
D . 2 3
Một khối lăng trụ có chiều cao 2a và diện tích đáy bằng 2 a 2 . Tính thể tích khối lăng trụ.
A. V = 4 a 3
B. V = 4 a 3 3
C. V = 2 a 3 3
D. V = 4 a 2 3
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Biết đường chéo cùa mặt bên là a 3 Khi đó, thể tích khối làng trụ bằng:
A. a 3 3
B. a 3 2
C. a 3 2 3
D. 2 a 3
Một lăng trụ đứng có đáy là tam giác đều cạnh a, cạnh bên bằng b. Khi đó thể tích V của khối lăng trụ đó là