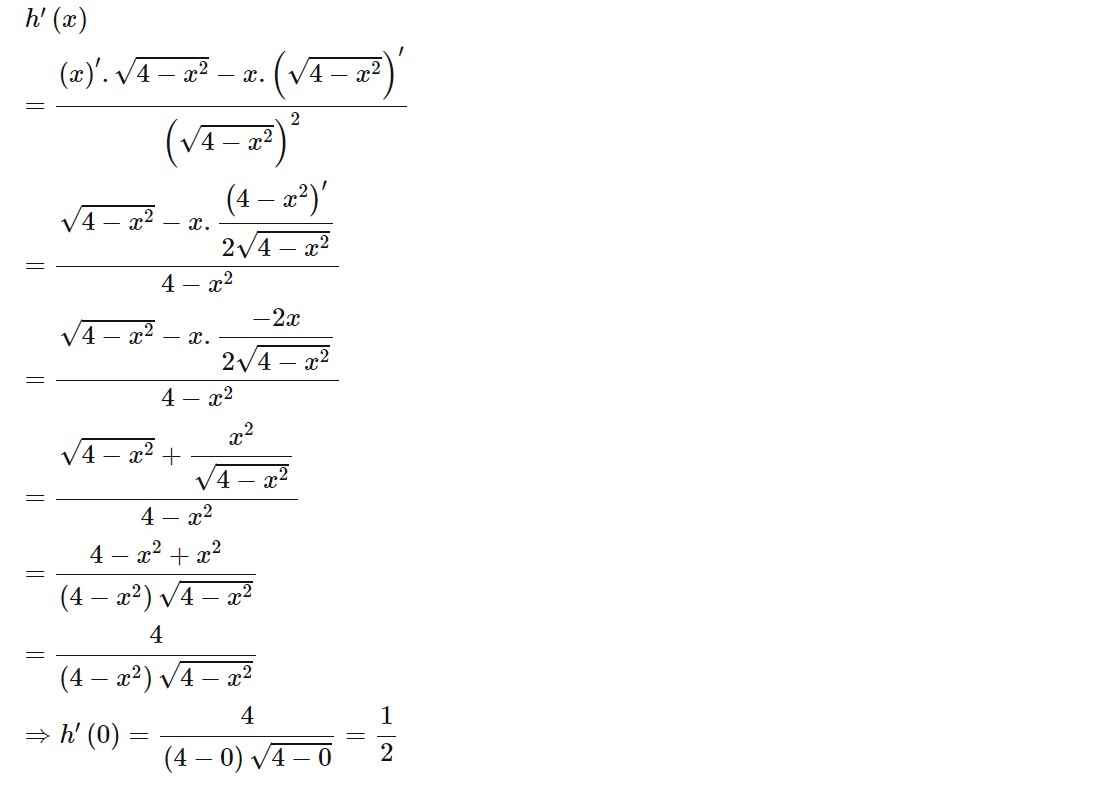Bài 2: Quy tắc tính đạo hàm
Các câu hỏi tương tự
Tính \(g'\left(1\right)\), biết rằng \(g\left(x\right)=\dfrac{1}{x}+\dfrac{1}{\sqrt{x}}+x^2\)
Rút gọn :
\(f\left(x\right)=\left(\dfrac{x-1}{2\left(\sqrt{x}+1\right)}+1\right)\left(\dfrac{2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x-2}}{\sqrt{x+2}+\sqrt{x-2}}+\dfrac{x+2}{\sqrt{x^2-4}-x+2}\right)\)
và tìm \(f'\left(x\right)\)
Tính \(\varphi'\left(2\right)\), biết rằng \(\varphi\left(x\right)=\dfrac{\left(x-2\right)\left(8-x\right)}{x^2}\)
Tính đạo hàm của hàm hợp:
a) y= \(\sqrt{\left(x^3-3x\right)^3}\)
b) y=\(\left(\sqrt{x^3+1}-x^2+2\right)^5\)
c) y= \(2.\left(x^6+2x-3\right)^7\)
d) y= \(\dfrac{1}{\sqrt{\left(x^3-1\right)^5}}\)
Giải các bất phương trình :
a) \(f'\left(x\right)>0\) với \(f\left(x\right)=\dfrac{1}{7}x^7-\dfrac{9}{4}x^4+8x-3\)
b) \(g'\left(x\right)\le0\) với \(g\left(x\right)=\dfrac{x^2-5x+4}{x-2}\)
c) \(\varphi'\left(x\right)< 0\) với \(\varphi\left(x\right)=\dfrac{2x-1}{x^2+1}\)
Cho f(x)=\(\sqrt{2+x}+\sqrt{7-x}-\sqrt{\left(2+x\right)\left(7-x\right)}\)
a, Tính đạo hàm của f(x)
b, Tìm những điểm mà tại đó đạo hàm bằng 0 hoặc không xác định
BT
28 tháng 3 2017 lúc 0:54
tính đạo hàm của mỗi hàm số sau :
a) y=\(\dfrac{1}{\left(x^2-x+1\right)^5}\) ; b) y=\(x^2+x\sqrt{x}+1\) ; c) y=\(\sqrt{\dfrac{x^2+1}{x}}\)
Tính \(f'\left(-1\right)\) biết \(f\left(x\right)=\dfrac{1}{x}+\dfrac{2}{x^2}+\dfrac{3}{x^3}\)
Cho \(f\left(x\right)=2x^3-x^2+\sqrt{3};g\left(x\right)=x^3+\dfrac{x^2}{2}-\sqrt{3}\)
Giải bất phương trình :
\(f'\left(x\right)>g'\left(x\right)\)