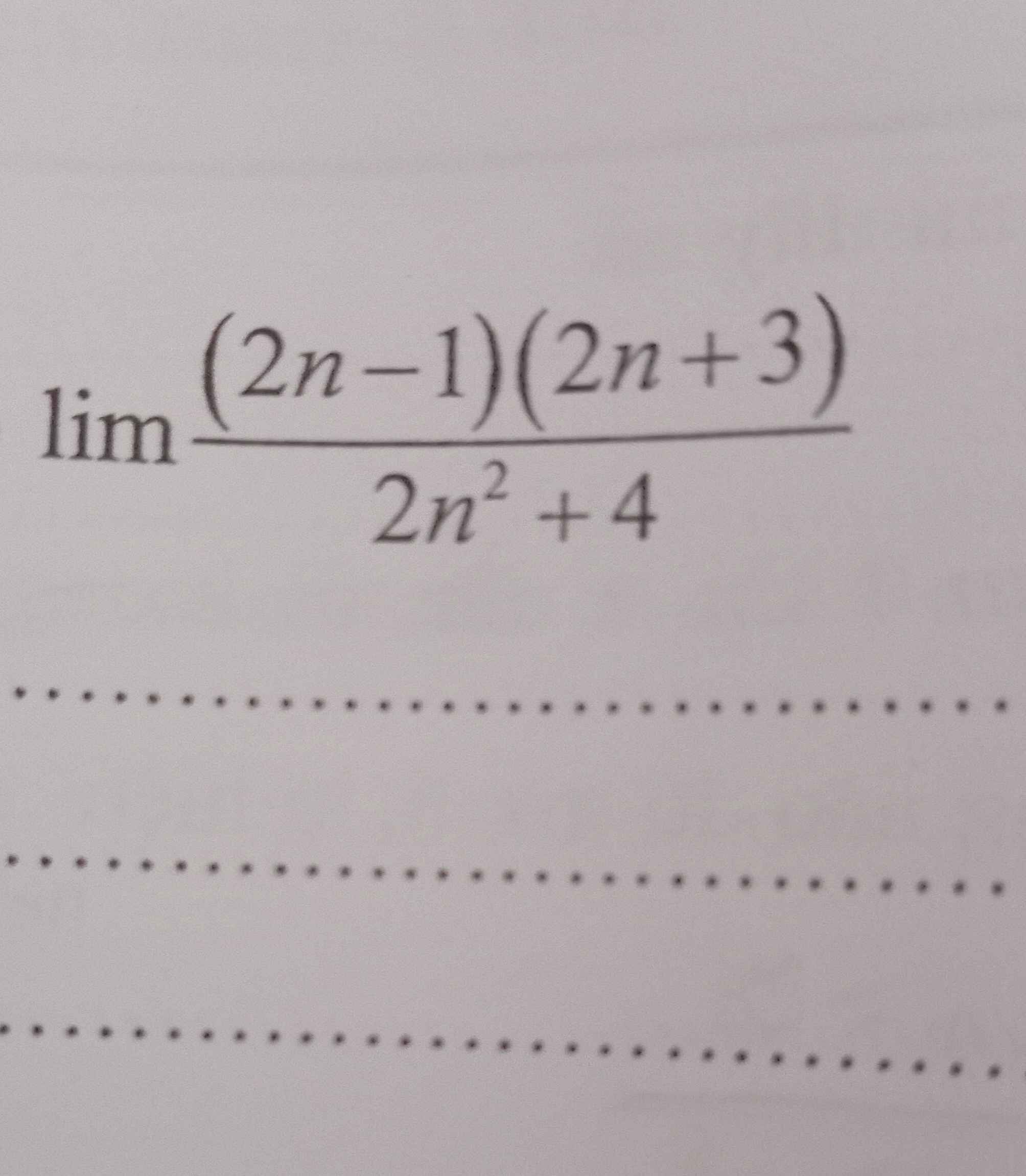\(\lim\limits\dfrac{\left(2n-1\right)\left(2n+3\right)}{2n^2+4}\)
\(=\lim\limits\dfrac{4n^2+6n-2n-3}{2n^2+4}\)
\(=\lim\limits\dfrac{4n^2+4n-3}{2n^2+4}\)
\(=\lim\limits\dfrac{4+\dfrac{4}{n}-\dfrac{3}{n^2}}{2+\dfrac{4}{n^2}}=\dfrac{4}{2}=2\)
\(...=\lim\limits_{n\rightarrow\infty}\dfrac{4n^2+4n-3}{2n^2+4}=\)\(\lim\limits_{n\rightarrow\infty}\dfrac{n^2\left(4+\dfrac{4}{n}-\dfrac{3}{n^2}\right)}{n^2\left(2+\dfrac{4}{n^2}\right)}\)
\(=\lim\limits_{n\rightarrow\infty}\dfrac{4+\dfrac{4}{n}-\dfrac{3}{n^2}}{2+\dfrac{4}{n^2}}=\dfrac{4}{2}=2\)