Đáp án B
Ta có y = log 2 ( 2 x + 1 ) → y ' = 2 x + 1 ' 2 x + 1 . ln 2 = 2 2 x + . ln 2 .
Đáp án B
Ta có y = log 2 ( 2 x + 1 ) → y ' = 2 x + 1 ' 2 x + 1 . ln 2 = 2 2 x + . ln 2 .
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
tính đạo hàm sau
\(y=ln\left(\frac{1-x^2}{1+x^2}\right)\)
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
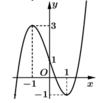
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Tính đạo hàm của hàm số y = ln ( x + x 2 + 1 )
A. y ' = 1 x + x 2 + 1
B. y ' = 1 x 2 + 1
C. y ' = x + x 2 + 1
d. y ' = x x + x 2 + 1
Tính đạo hàm của hàm số y = ln ( x 2 + 1 - x )
A. y ' = - 1 x 2 + 1 - x
B. y ' = - 1 x 2 + 1
C. y ' = 1 x 2 + 1
D. y ' = x x 2 + 1
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f - 1 = 1 ; f - 1 e = 2 . Bất phương trình f x < ln - x + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
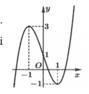
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Hệ số góc của tiếp tuyến với đồ thị hàm số y = ln(x+1) tại điểm có hoành độ x = 2 là
A. 1 3 ln 2
B. 1
C. ln2
D. 1 3
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Tìm khoảng nghịch biến của đồ thị hàm số y=f(x)
A. (∞;0) và (1;2)
B. (0;1)
C. (0;2)
D. (2;+∞)
Tính đạo hàm của hàm số y = ( x - 2 ) x 2 + 1
A. y ' = 2 x 2 - 2 x - 1 x 2 + 1
B. y ' = 2 x 2 + 2 x + 1 x 2 + 1
C. y ' = 2 x 2 - 2 x + 1 x 2 - 1
D. y ' = 2 x 2 - 2 x + 1 x 2 + 1
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x 2 − 1 ) 2 ( x + 2 ) 3 . Khi đó số điểm cực trị của hàm số y = f x 2 là bao nhiêu?
A. 1
B. 2
C. 3
D. 4