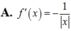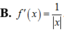ta có:
\(y'=\frac{\left(\frac{1-x^2}{1+x^2}\right)'}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-2x.\left(1+x^2\right)-2x.\left(1-x^2\right)}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-4x}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{-4x}{\left(1+x^2\right)\left(1-x^2\right)}=\frac{-4x}{1-x^4}\)
tính đạo hàm
\(ln\left(x+\sqrt{x^2+1}\right)\)
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Tính đạo hàm của hàm số y = ln ( x + x 2 + 1 )
A. y ' = 1 x + x 2 + 1
B. y ' = 1 x 2 + 1
C. y ' = x + x 2 + 1
d. y ' = x x + x 2 + 1
Tính đạo hàm của hàm số y = ln ( x 2 + 1 - x )
A. y ' = - 1 x 2 + 1 - x
B. y ' = - 1 x 2 + 1
C. y ' = 1 x 2 + 1
D. y ' = x x 2 + 1
tìm giá trị nhỏ nhất và lớn nhất của hàm số sau
\(y=\frac{x^2-x+1}{x-1}\) trên \(\left[-2;\frac{1}{2}\right]\)
CHO x;y thuộc Z và x;y khác 0
thỏa mãn \(\frac{x^2}{y^2}+\frac{y^2}{x^2}+2\left(x+y\right)-3\left(\frac{x}{y}+\frac{y}{x}\right)+3\left(\frac{1}{x}+\frac{1}{y}\right)-\frac{2}{xy}=4\)
TÍNH E=x+y
Tính đạo hàm của hàm số f(x)=ln x
Đề này dùng để cho các bạn lớp 7 tham khảo , không cần giải , bài nào không biết thì nói với mình
Câu 1: Tính
\(A=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)....\left(1-\frac{1}{2013}\right)\left(1-\frac{1}{2014}\right)\)
\(B=\frac{2^{12}.3^5-4^6.9^2}{\left(2^2.3\right)^6+8^4.3^5}-\frac{5^{10}.7^3-25^5.49^2}{\left(125.7\right)^3+5^9.14^3}\)
Câu 2: Cho \(\frac{2x+2y-z}{z}=\frac{2x+2z-y}{y}=\frac{2z+2y-x}{x}\) (với x,y,z là các số hữu tỉ dương)
Tính giá trị của \(C=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{8xyz}\)
Giải hệ pt:
1.\(\sqrt[4]{x}\left(\left\{\left\{\frac{1}{4}+\frac{2\sqrt{x}+\sqrt{y}}{x+y}\right\}\right\}\right)=2\)
2.\(\sqrt[4]{y}\left(\frac{1}{4}-\frac{2\sqrt{x}+\sqrt{y}}{x+y}\right)=1\)
SOS