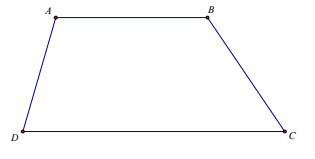
Vì `AB //// CD`
$\bullet$ `\hat{A}+\hat{D}=180^o`
`=>3\hat{D}+\hat{D}=180^o`
`=>4\hat{D}=180^o`
`=>\hat{D}=45^o`
`=>\hat{A}=3.45^o =135^o`
$\bullet$ `\hat{B}+\hat{C}=180^o`
`=>\hat{B}=180^o -\hat{C}`
Mà `\hat{B}-\hat{C}=30^o`
`=>180^o -\hat{C}-\hat{C}=30^o`
`=>2\hat{C}=150^o=>\hat{C}=75^o`
`=>\hat{B}=180^o -75^o =105^o`
`{(A = 3D), (hatA + hatD = 180^o):}`
`=> 4hatD = 180^o`
`=> hatD = 45^o`
`=> hatA = 135^o`
`{(hatB-hatC = 30^o), (hatB +hatC = 180^o):}`
`=> hat B = (180^o + 30^o) : 2 = 105^o`
`=> hat C = 180^o - 115^o = 75^o`
Ta có:`AB////CD`
\(\Rightarrow\widehat{A}+\widehat{D}=180^o\) ( trong cùng phía )
\(\Rightarrow3\widehat{D}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{D}=45^o\)
\(\Rightarrow\widehat{A}=3.45^o=135^o\)
\(\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}+30^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=75^o\)
\(\Rightarrow\widehat{B}=30^o+75^o=105^o\)
Vậy \(\left\{{}\begin{matrix}A=135^o\\B=105^o\\C=75^o\\D=45^o\end{matrix}\right.\)