\(x^3-3x+2-2m=0\)
=>\(2m=x^3-3x+2\)
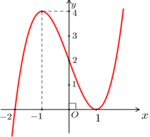
Chúng ta sẽ vẽ đồ thị \(y=x^3-3x+2\)
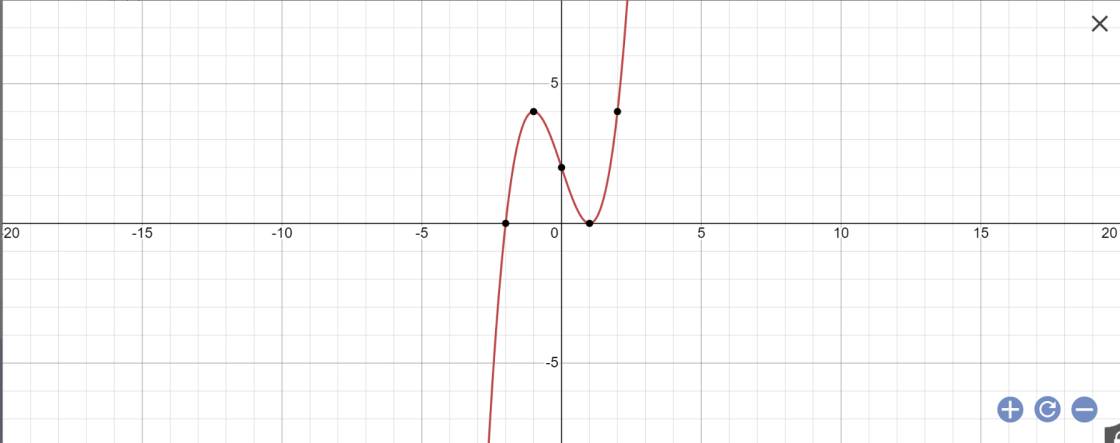
Trên đồ thị, chúng ta sẽ thấy khi \(y\in\left(0;4\right)\) thì \(y=x^3-3x+2\) sẽ cho 3 nghiệm phân biệt
=>\(2m\in\left(0;4\right)\)
=>\(m\in\left(0;2\right)\)
=>Chọn B
\(x^3-3x+2-2m=0\)
=>\(2m=x^3-3x+2\)
Chúng ta sẽ vẽ đồ thị \(y=x^3-3x+2\)

Trên đồ thị, chúng ta sẽ thấy khi \(y\in\left(0;4\right)\) thì \(y=x^3-3x+2\) sẽ cho 3 nghiệm phân biệt
=>\(2m\in\left(0;4\right)\)
=>\(m\in\left(0;2\right)\)
=>Chọn B
Tìm tất cả các giá trị thực của tham số m để phương trình 9 x - m . 3 x + 2 m - 5 = 0 có hai nghiệm trái dấu
![]()
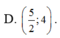
Cho hàm số y = x 3 - 3 x + 2 có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x + 2 - 2 m = 0 có ba nghiệm thực phân biệt.
A. 0<m<4
B. 0<m<2
C. 0 ≤ m ≤ 4
D. 0 ≤ m ≤ 2
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x 2 - 3 x + 2 ≤ 0 cũng là nghiệm của bất phương trình m x 2 + ( m + 1 ) x + m + 1 ≥ 0 ?
A. m ≤ - 1 .
B. m ≤ - 4 7 .
C. m ≥ - 4 7 .
D. m ≥ - 1 .
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0
A. m ≤ - 1
B. m ≤ - 4 7
C. m ≥ - 4 7
D. m ≥ - 1
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx2+ (m+ 1) x+ m+1≥0?
A. m< -1
B. m ≤ - 4 7 .
C. m ≥ - 4 7 .
D. m> -1
Tìm tất cả các giá trị thực của tham số m để bất phương trình log0,02[log2 (3x + 1)] > log0,02 m có nghiệm với mọi x ∈ - ∞ ; 0 .
A. m > 9
B. m < 2
C. 0 < m < 1
D. m ≥ 1
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Tìm tất cả các giá trị của tham số thực m để phương trình log 3 2 x - 3 log 3 x + 2 m - 7 = 0 có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) = 72.
A. m = 61 2
B. m = 3
C. K h ô n g t ồ n t ạ i
D. m = 9 2
Cho hàm số y=f(x) có đạo hàm liên tục trên R, với f x > 0 , ∀ x ∈ ℝ và f 0 = 1 . Biết rằng f ' x + 3 x x − 2 f x = 0 , ∀ x ∈ ℝ . Tìm tất cả các giá trị thực của tham số m để phương trình f x + m = 0 có bốn nghiệm thực phân biệt.
A. 1 < m < e 4 .
B. − e 6 < m < − 1.
C. − e 4 < m < − 1.
D. 0 < m < e 4 .