+ Đạo hàm y’ = 3x2- 6mx= 3x( x- 2m)
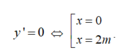
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi :m≠0. (1)
+ Tọa độ các điểm cực trị của đồ thị hàm số là A( 0 ; 3m3) ; B( 2m; -m3)
Ta có: O A → ( 0 ; 3 m 3 ) ⇒ O A = 3 m 3 ( 2 )
Ta thấy A ∈ O y ⇒ O A ≡ O y ⇒ d ( B ; O A ) = d ( B ; O y ) = 2 m (3)
+ Từ (2) và (3) suy ra S= ½. OA.d(B ; OA)=3m4.
Do đó: S ∆ O A B = 48 ⇔ 3 m 4 = 48 ⇔ m = ± 2 (thỏa mãn (1) ).
Chọn D.

