Question

Tìm số tự nhiên n sao cho: (4n+7) chia hết cho (n+1)

Tìm số nguyên n thỏa mãn: (6n-5) chia hết cho (2n-1)

tìm các số tự nhiên n, biết n + 2 chia hết cho 5 - 3n 

Giải nhanh giúp mk với

Answer 1

a) ( 4n + 7 ) ⋮ ( n + 1 )

⇒ 4.( n + 1 ) + 3 ⋮ ( n + 1 )

Vì 4.( n + 1 ) ⋮ ( n + 1 )

nên 3 ⋮ ( n + 1 )

⇒ ( n + 1 ) \(\in\) Ư(3)

( n + 1 ) \(\in\) { 1 ; 3 } ( Do n \(\in\) N )

n \(\in\) { 0 ; 2 }

b) ( 6n - 5 ) ⋮ ( 2n - 1 )

⇒ 3.( 2n - 1 ) + 2 ⋮ ( 2n - 1 )

Vì 3.( 2n - 1 ) ⋮ ( 2n - 1 )

nên 2 ⋮ ( 2n - 1 )

⇒ ( 2n - 1 ) \(\in\) Ư(2)

( 2n - 1 ) \(\in\) { 1 ; 2 ) ( Do n \(\in\) N )

2n \(\in\) { 2 ; 3 }

n \(\in\) { 1 ; loại }

Vậy n = 1

Answer 2

(4n + 7) ⋮ (n + 1)

⇒ (4n + 4 + 3) ⋮ (n + 1)

⇒ [4(n + 1) + 3] ⋮ (n + 1)

⇒ 3 ⋮ (n + 1)

⇒ n + 1 ∈ Ư(3) = {-3; -1; 1; 3}

⇒ n ∈ {-4; -2; 0; 2}

Mà n ∈ ℕ

⇒ n ∈ {0; 2}

Vậy n ∈ {0; 2}

------------

(6n - 5) ⋮ (2n - 1)

⇒ (6n - 3 - 2) ⋮ (2n - 1)

⇒ [3(2n - 1) - 2] ⋮ (2n - 1)

⇒ 2 ⋮ (2n - 1)

⇒ 2n - 1 ∈ Ư(2) = {-2; -1; 1; 2}

⇒ 2n ∈ {-1; 0; 2; 3}

Do n ∈ Z ⇒ 2n là số chẵn

⇒ 2n ∈ {0; 2}

⇒ n ∈ {0; 1}

Vậy n ∈ {0; 1}

------------

(n + 2) ⋮ (5 - 3n)

⇒ (n + 2) ⋮ (3n - 5)

⇒ 3(n + 2) ⋮ (3n - 5)

⇒ (3n + 6) ⋮ (3n - 5)

⇒ (3n - 5 + 11) ⋮ (3n - 5)

⇒ 11 ⋮ (3n - 5)

⇒ 3n - 5 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ 3n ∈ {-6; -4; 6; 16}

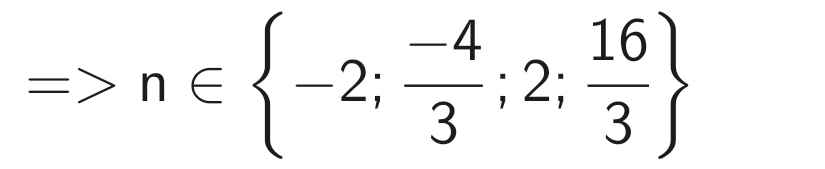
Mà n ∈ ℕ

⇒ n = 2

Vậy n = 2