Đáp án C.
Phương trình hoành dộ giao điểm là
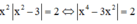
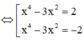
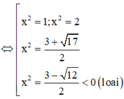
=> PT có 6 nghiệm
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án C.
Phương trình hoành dộ giao điểm là
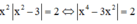
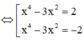
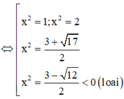
=> PT có 6 nghiệm
Gọi M, N là các giao điểm của đường thẳng y = x − 4 với đồ thị của hàm số y = − 2 x + 5 x − 2 . Tìm tọa độ trung điểm I của MN?
A. I 2 ; − 2
B. I 1 ; − 3
C. I 3 ; − 1
D. I − 2 ; 2
Gọi M;N là giao điểm của đồ thị hàm số và đường thẳng y = x + 2 . Khi đó tung độ trung điểm I của đoạn MN bằng bao nhiêu?
A. − 3 2
B. 11 2
C. 7 2
D. − 7 2
Khi đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A, B và đường tròn (C): ( x - 1 ) 2 + ( y - 1 ) 2 = 3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN
A. MN= 3
B. MN=1.
C. MN=2.
D. MN=2 3
Tìm số giao điểm n của đồ thị hai hàm số sau: y = x 4 − 3 x 2 + 2 và y = x 2 − 2
A. n = 2
B. n = 0
C. n = 4
D. n = 1
Cho hàm số y = x 3 - 3 x + 2 C . Biết rằng đường thẳng d : y = a x + b cắt đồ thị C tại ba điểm phân biệt M, N, P. Tiếp tuyến tại ba điểm M, N, P của đồ thị C cắt C tại các điểm M ' , N ' , P ' (tương ứng khác M, N, P). Khi đó đường thẳng đi qua ba điểm M ' , N ' , P ' có phương trình là
A. y = 4 a + 9 x + 18 - 8 b
B. y = 4 a + 9 x + 14 - 8 b
C. y = a x + b
D. y = - 8 a + 18 x + 18 - 8 b
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 − 2 x 2 + 2 v à y = − x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)
Tìm hoành độ của giao điểm của đồ thị hàm số y = x 2 + x + 3 x - 2 và đường thẳng y = x
A. x = 1
B. x = 3
C. x = 0
D. x = -1
Cho hàm số y = x 3 + x + 2 có đồ thị (C). Số giao điểm của (C) và đường thẳng y = 2 là:
A. 1.
B. 0.
C. 3.
D. 2.
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)