Question

Tìm số a để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.

Answer 1

Thực hiện phép chia:

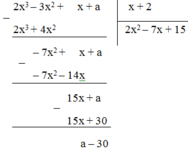
2x3 – 3x2 + x + a chia hết cho x + 2

⇔ số dư = a – 30 = 0

⇔ a = 30.

Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.

2x3 – 3x2 + x + a

= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30

(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)

= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30

= (2x2 – 7x + 15)(x + 2) + a – 30

2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.