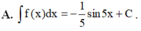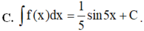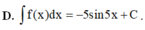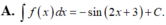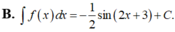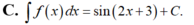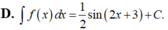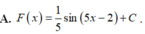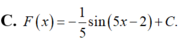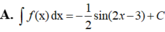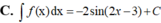Question

Tìm nguyên hàm của 1/cos x

Answer 1

\(\int\dfrac{1}{cosx}dx=\int\dfrac{cosx}{cos^2x}dx=\int\dfrac{cosx}{1-sin^2x}dx=-\int\dfrac{cosx}{sin^2x-1}dx\)

\(=-\int\dfrac{cosx}{\left(sinx-1\right)\left(sinx+1\right)}dx=-\dfrac{1}{2}\int\left(\dfrac{1}{sinx-1}-\dfrac{1}{sinx+1}\right)d\left(sinx\right)\)

\(=-\dfrac{1}{2}\left[ln\left|sinx-1\right|-ln\left|sinx+1\right|\right]+C=\dfrac{1}{2}ln\left|\dfrac{sinx+1}{sinx-1}\right|+C\)