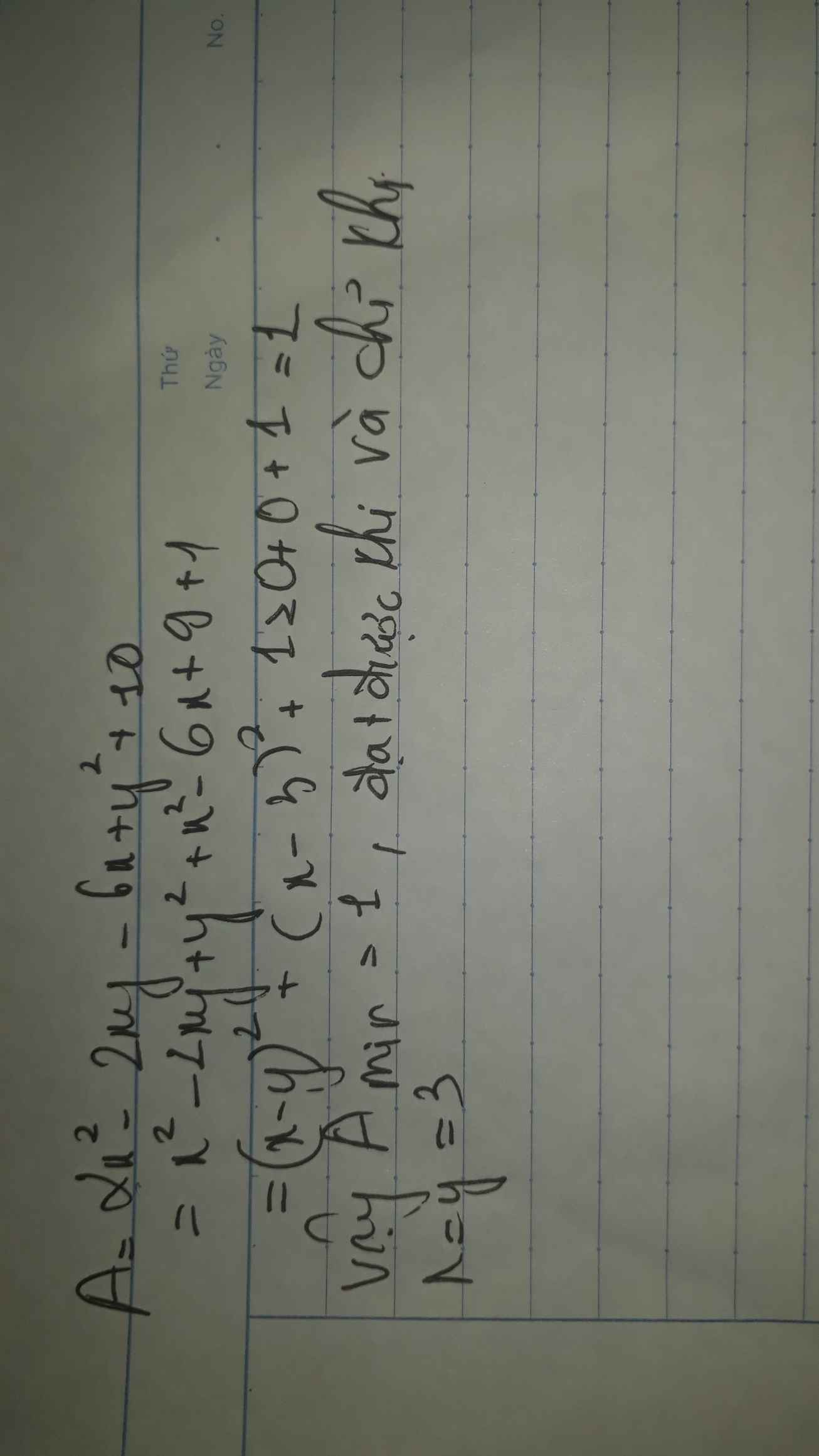`A=2x^2-2xy-6x+y^2+10`
`A=x^2-2xy+y^2+x^2-6x+10`
`A=(x-y)^2+x^2-6x+9+1`
`A=(x-y)^2+(x-3)^2+1`
Vì `(x-y)^2+(x-3)^2>=0=>A>=1`
Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`
A=\(\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\\ \)
dấu= xảy ra khi x=y=3
tick mik nha
Ta có: \(A=2x^2-2xy-6x+y^2+10\)
\(=\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1\)
\(=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\forall x,y\)
Dấu '=' xảy ra khi x=y=3
A=2x2-2xy-6x+y2+10
=(x^2 -2xy+y^2)+(x^2-6x+9)+1
=(x-y)^2+(x-3)^2+1>=1