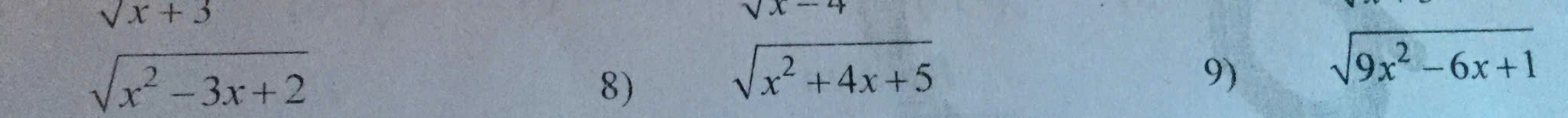7: ĐKXĐ: \(x^2-3x+2>=0\)
=>(x-1)(x-2)>=0
TH1: \(\left\{{}\begin{matrix}x-1>=0\\x-2>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=1\\x>=2\end{matrix}\right.\)
=>x>=2
TH2: \(\left\{{}\begin{matrix}x-1< =0\\x-2< =0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =1\\x< =2\end{matrix}\right.\)
=>x<=1
9: ĐKXĐ: \(9x^2-6x+1>=0\)
=>\(\left(3x-1\right)^2>=0\)(luôn đúng)
=>\(x\in R\)
8: ĐKXĐ: \(x^2+4x+5>=0\)
=>\(x^2+4x+4+1>=0\)
=>\(\left(x+2\right)^2+1>=0\)(luôn đúng)
=>\(x\in R\)
7) \(\dfrac{\sqrt{x+3}}{\sqrt{x^2-3x+2}}xđ\Leftrightarrow\left\{{}\begin{matrix}x+3\ge0\\x^2-3x+2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\\left(x-1\right)\left(x-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x< 1\cup x>2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}-3\le x< 1\\x>2\end{matrix}\right.\)
Vậy đkxđ là \(\left[{}\begin{matrix}-3\le x< 1\\x>2\end{matrix}\right.\)
8) \(\sqrt{x^2+4x+5}xđ\Leftrightarrow x^2+4x+5\ge0,\forall x\in R\) vì \(\left(\Delta'=-1< 0;1>0\right)\)
Vậy đkxđ là \(\forall x\in R\)
9) \(\sqrt{9x^2-6x+1}xđ\Leftrightarrow9x^2-6x+1\ge0\)
\(\Leftrightarrow\left(3x-1\right)^2\ge0,\forall x\in R\)
Vậy đkxđ là \(\forall x\in R\)