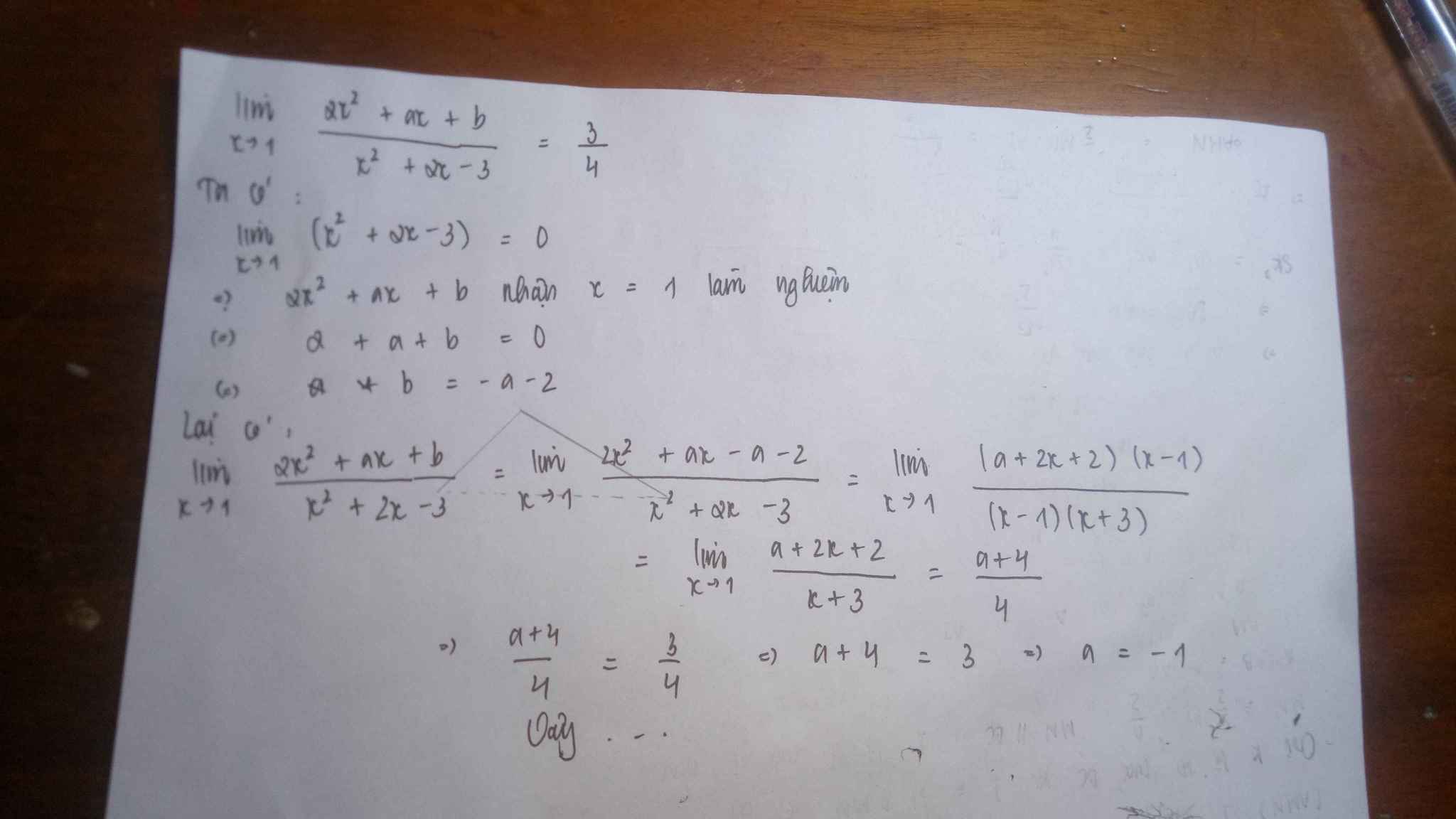\(x^2+2x-3=0\) có nghiệm \(x=1\) nên giới hạn đã cho hữu hạn khi \(2x^2+ax+b=0\) cũng có nghiệm \(x=1\)
\(\Rightarrow2.1^2+a.1+b=0\Rightarrow a+b+2=0\Rightarrow b=-a-2\)
Thay vào:
\(\lim\limits_{x\rightarrow1}\dfrac{2x^2+ax-a-2}{x^2+2x-3}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2\right)+a\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2+a\right)}{\left(x-1\right)\left(x+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{2x+2+a}{x+3}=\dfrac{4+a}{4}=\dfrac{3}{4}\)
\(\Rightarrow4+a=3\Rightarrow a=-1\Rightarrow b=-a-2=-1\)