Tập xác định: D = R \ {1}
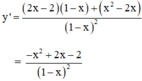
y’ < 0 với ∀ x ∈ D (vì –x2 + 2x – 2 < 0).
y' không xác định tại x = 1
Bảng biến thiên:
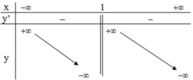
Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞)
Tập xác định: D = R \ {1}
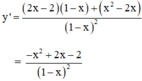
y’ < 0 với ∀ x ∈ D (vì –x2 + 2x – 2 < 0).
y' không xác định tại x = 1
Bảng biến thiên:

Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞)
Tìm các khoảng đơn điệu của hàm số y=x²+2x+2/x+1
Tìm các khoảng đơn điệu của các hàm số: y = 3 x + 1 1 - x
Tìm các khoảng đơn điệu của các hàm số: y = x 2 - x - 20
Phát biểu các điều kiện đồng biến và nghịch biến của hàm số. Tìm các khoảng đơn điệu của hàm số
y = - x 3 + 2 x 2 - x - 7 ; y = x - 5 1 - x
Tìm các khoảng đơn điệu của các hàm số:
y = 2 x x 2 - 9
Cho hàm số y= f(x) là hàm số đơn điệu trên khoảng (a; b). Trong các khẳng định sau, khẳng định nào đúng?
![]()
![]()
![]()
D. f'(x) không đổi dấu trên (a;b)
Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Xét tính đơn điệu của các hàm số sau:
\(y = {x^2 -1 \over x^2 +1} trong ( 0; + vô cùng)\)
\(y = {x^4-4x^3 \over x-1} \)
\(y = { \sqrt{x} -x}\)
\(y={x^2\over\sqrt {x^2-1}}\)
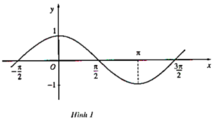
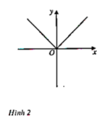
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [(-π)/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞)