Trên hình 13a ta có:
= ; = = vì ≠ nên ≠ => PM và MC không song song.
Ta có => MN//AB
Trong hình 13b
Ta có: = ; = =
Đúng 1
Bình luận (0)
tìm các cặp đường thẳng song song trong h.10 và giải thích vì sao chúng song song
: Cho hình thang ABCD (AB < CD và AB // CD). Vẽ qua A đường thẳng AK song song với BC (K DC) và AK cắt BD tại E, vẽ qua B đường thẳng BI song song với AD (I CD) cắt AC tại F.
a) Chứng minh rằng: EF // AB
b) Chứng minh rằng: AB2 = CD.EF
Cho hình thang ABCD (AB // CD) có O là giao điểm của hai đường chéo AC và BD. Qua A, kẻ đường thẳng song song với BC cắt BD tại E. Qua B, kẻ đường thẳng song song với AD cắt AC tại F.
a) Chứng minh: EF // CD.
b) Chứng minh: AB2 = CD . EF
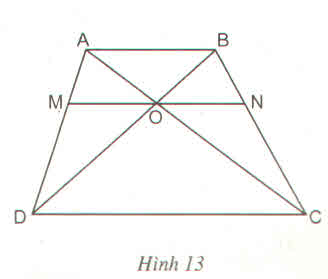
Hình thang ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON (h.13)
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh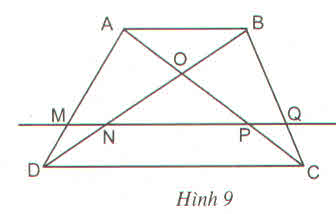 
DN\BD=CP\AC
Cho tứ giác ABCD. Qua E thuộc cạnh AD, kẻ đường thẳng song song với DC cắt AC tại G. Qua G kẻ đường thẳng song song CB cắt AB tại H. a. Chứng minh: HE song song BD. b. Qua B kẻ đường thẳng song song với CD cắt AC tại I. Qua C kẻ đường thẳng song song với BA cắt BA tại F. Chứng minh: IF song song AD.
Gọi O là giao điểm của hai đường thẳng chưa cạnh AD và BC của hình thang ABCD. Đường thằng đi qua O và song song với AB cắt các đường thẳng AC, BD lần lượt tại M, N. CM: OM = ON
giúp e với e đang cần gấp ạ
Bài 1. Cho DABC, kẻ phân giác trong và ngoài của góc B cắt AC ở I và D. Từ C kẻ đường thẳng song song với AB cắt BI, BD lần lượt tại E, F.
a) Chứng minh IB.IC = IA.IE;
b) Chứng minh CE = CF.
c) Từ I, D kẻ đường thẳng song song với BC cắt đường thẳng AB lần lượt tại M, N. Tính độ dài AB, MN; EF nếu MI = 4cm và BC = 12cm.
Cho tam giác ABC có O nằm trong tam giác. Đường thẳng qua O song song với BC cắt AB,AC tại M,N. Đường thẳng qua O song song với AB cắt AC, BC tại F, E. Đường thẳng qua O song song với AC cắt AB, BC tại I, K.
Chứng minh: \(\dfrac{AI}{AB}+\dfrac{BE}{BC}+\dfrac{CN}{AC}=1\)
