Các câu hỏi tương tự
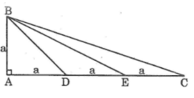
Tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC
Chứng minh tam giác BDE đồng dạng tam giác CDB
Tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC
Chứng minh DE/DB = DB/DC
Cho tam giác ABC vuông tại A, AC3AB Các điểm D và E thuộc cạnh AC sao cho AD DE EC. Gọi M là điểm đối cứng với B qua D. Chứng minh rằng:1) ABCM là tứ giác nội tiếp 2)GÓC ACB+GÓC AEB ^{45^o}
Đọc tiếp
Cho tam giác ABC vuông tại A, AC=3AB Các điểm D và E thuộc cạnh AC sao cho AD = DE = EC. Gọi M là điểm đối cứng với B qua D. Chứng minh rằng:
1) ABCM là tứ giác nội tiếp 2)GÓC ACB+GÓC AEB= \(^{45^o}\)
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)a) Chứng minh AD là trung trực của đoạn EF.[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DGDE. Chứng minh tam giác CEG vuông.Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nh...
Đọc tiếp
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.
Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)
a) Chứng minh AD là trung trực của đoạn EF.
[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DG=DE. Chứng minh tam giác CEG vuông.
Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Vẽ tam giác vuông cân CBG cân tại B,G và A ở cùng nửa mặt phẳng bờ là đường thẳng BC. Chứng minh rằng GA vuông góc vớ DC.
Bài 4.Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là trung điểm của các đoạn BC,PQ. Đường thẳng MN cắt đường thẩngB,AC theo thứ tự tại B' và C'. Chứng minh rằng tam giác B'AC cân.
Cho tam giác ABC vuông tại A có ABa, AC3a. Trên AC lấy các các điểm D và E sao cho ADDEEC.a Chứng minhfrac{DE}{DB}frac{DB}{DC}b Chứng minh tam giác BDE đồng dạng tam giác CBD.4 Cho tam giác ABC cân tại A (A90o). Kẻ BM vuông góc với CACMR: frac{AM}{MC}2(frac{AB}{AC})2 - 1
Đọc tiếp
Cho tam giác ABC vuông tại A có AB=a, AC=3a. Trên AC lấy các các điểm D và E sao cho AD=DE=EC.
a Chứng minh\(\frac{DE}{DB}\)=\(\frac{DB}{DC}\)
b Chứng minh tam giác BDE đồng dạng tam giác CBD.
4 Cho tam giác ABC cân tại A (A<90o). Kẻ BM vuông góc với CA
CMR: \(\frac{AM}{MC}\)=2(\(\frac{AB}{AC}\))2 - 1
cho tam giác ABC vuông tại A, AB=a,AC=3a.Trên AC lấy D,E sao cho AD=DE=EC.
a) CMR:\(\frac{DE}{DB}=\frac{DB}{DC}\)
b) tam giác BDE đồng dạng với tam giác CDB
c) tính tổng: góc ACE+ góc BCD
Cho tam giác ABC có AB = 6, AC = 8, BC =10.
a/ Chứng minh tam giác ABC vuông
b/ Lấy điểm D trên cạnh AB sao cho BD = 2. Từ D kẻ DE // BC ( E thuộc AC). Tính DE, EC?
1 Hình vuông ABCD có cạnh AB=a. Gọi M là trung điểm của cạnh BC. Trên cạnh CD ta lấy điểm N sao cho khoảng cách từ đó đến đường thẳng AM bằng độ dài đoạn thẳng DN. Tính độ dài các đoạn thẳng AM, CN, MN
2 Cho tam giác vuông ABC vuông tại B có AB=3a, BC=4a. Ta dựng tam giác ACD vuông cân tại D sao cho D khác phía với B đối vớ đường thẳng AC. Tính độ dài AD,BD
Cho tam giác ABC có AB=4cm. Điểm D trên cạnh AB sao cho AD=3cm. Lấy điểm E trên cạnh AC sao cho DE song song BC. Giả sử AE+AC=14cm. Tính tỉ số giữa AE và AC rồi tính độ dài AE, EC, AC.