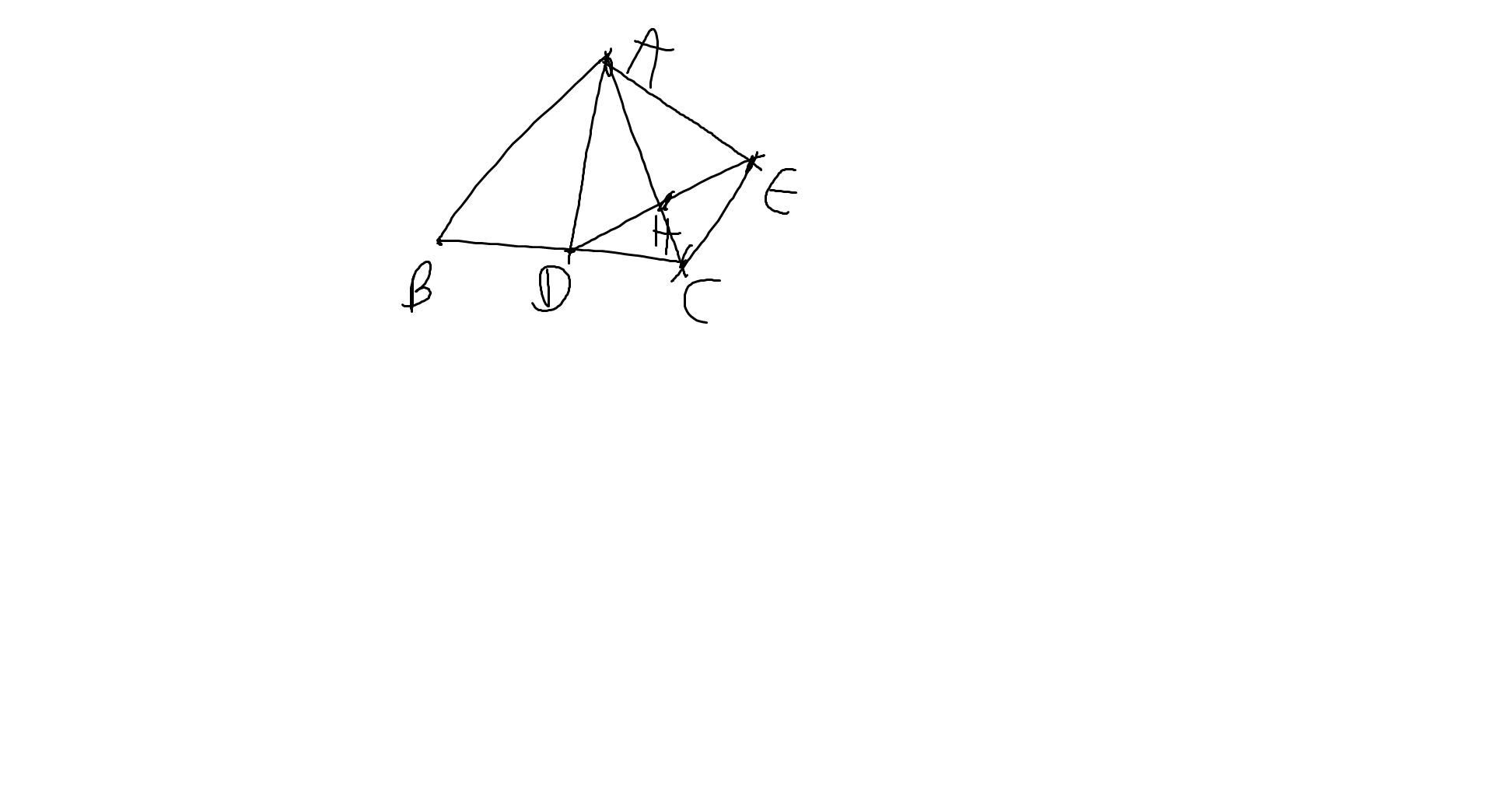Question

tam giác abc có ab=ac. tia phân giác của góc a cắt bc tại d

a)cm db=dc

b)cm ad vuông góc bc

c) vẽ dh vuônn góc ac(h thuộc ac).trên tia đối của tia hd lấy điểm e sao cho he=hd.cm góc ade=góc acb

d)cm ce vuông góc ae

(học sunh vẽ hình)

Answer 1

a: Xét ΔADB và ΔADC có

AB=AC

\(\widehat{BAD}=\widehat{CAD}\)

AD chung

Do đó: ΔADB=ΔADC

b: ΔADB=ΔADC

=>\(\widehat{ADB}=\widehat{ADC}\)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

=>AD\(\perp\)BC

c: Ta có: \(\widehat{ADH}+\widehat{HAD}=90^0\)(ΔAHD vuông tại H)

\(\widehat{ACB}+\widehat{DAC}=90^0\)(ΔADC vuông tại D)

Do đó: \(\widehat{ADH}=\widehat{ACB}\)

d: Xét ΔAHD vuông tại H và ΔAHE vuông tại H có

AH chung

HD=HE

Do đó: ΔAHD=ΔAHE

=>\(\widehat{HAD}=\widehat{HAE}\) và AD=AE

Xét ΔADC và ΔAEC có 

AD=AE

\(\widehat{DAC}=\widehat{EAC}\)

AC chung

Do đó: ΔADC=ΔAEC

=>\(\widehat{ADC}=\widehat{AEC}\)

=>\(\widehat{AEC}=90^0\)

=>EC\(\perp\)EA