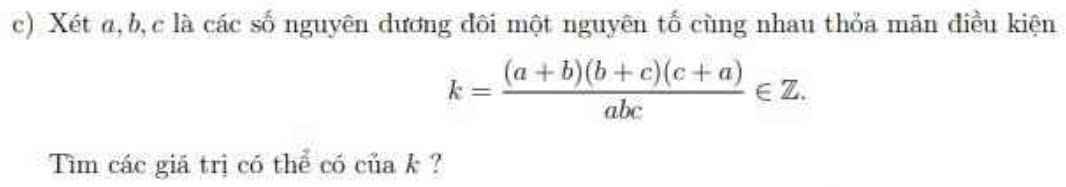Vai trò của a;b;c như nhau, ko mất tính tổng quát giả sử \(a\ge b\ge c\)
- Nếu \(a=b=c\Rightarrow a=b=c=1\Rightarrow k=8\)
- Nếu \(a;b;c\) có ít nhất 2 số khác nhau
Do a;b;c nguyên tố cùng nhau nên \(\left(a+b;a\right)=\left(a+c;a\right)=1\)
\(\Rightarrow b+c\) chia hết cho a
\(\Rightarrow b+c=a.x\)
\(\Rightarrow a.x< a+a=2a\)
\(\Rightarrow x< 2\Rightarrow x=1\)
\(\Rightarrow a=b+c\)
\(\Rightarrow k=\dfrac{\left(2b+c\right)\left(2c+b\right)}{bc}=\dfrac{2b}{c}+\dfrac{2c}{b}+5\)
Theo 1 bổ đề đã chứng minh, nếu \(\left\{{}\begin{matrix}\dfrac{x}{a}+\dfrac{y}{b}\in Z\\\left(a;b\right)=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{a}\in Z\\\dfrac{y}{b}\in Z\end{matrix}\right.\)
Do đó ta có \(\left\{{}\begin{matrix}\dfrac{2b}{c}\in Z\\\dfrac{2c}{b}\in Z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2⋮b\\2⋮c\end{matrix}\right.\) do \(\left(b;c\right)=1\)
\(\Rightarrow\left(b;c\right)=\left(2;2\right);\left(1;1\right);\left(2;1\right)\)
\(\Rightarrow\left(a;b;c\right)=\left(4;2;2\right);\left(2;1;1\right);\left(3;2;1\right)\)
\(\Rightarrow k=10;9\)
Tổng hợp lại ta có \(k=8;9;10\)