Ta có ∫ (xcosx)’dx = (xcosx) và ∫ cosxdx = sinx. Từ đó
∫ xsinxdx = - ∫ [(xcosx)’ – cosx]dx = -∫ (xcosx)’dx + ∫ cosxdx = - xcosx + sinx + C.
Biết I = ∫ 0 π 2 x + x cos x - sin 3 x 1 + cos x d x = π 2 a - b c . Trong đó a, b, c là các số nguyên dương, phân số b c tối giản. Tính T = a 2 + b 2 + c 2
Biết ∫ 0 π 2 x + x cos x - sin 3 x 1 + cos x d x = π 2 3 - b c Trong đó a, b, c là các số nguyên dương, phân số b/c tối giản. Tính T = a 2 + b 2 + c 2
A. T =16
B. T = 59
C. T =69
D. T = 50
Tìm nguyên hàm của hàm số f ( x ) = x cos x
A. ∫ f ( x ) d x = x sin x - cos x + C
B. ∫ f ( x ) d x = - x sin x - cos x + C
C. ∫ f ( x ) d x = x sin x + cos x + C
D. ∫ f ( x ) d x = - x sin x + cos x + C
Cho ∫ 0 π f ( x ) d x = 2 và ∫ 0 π g ( x ) d x = - 1 . Tính I= ∫ 0 π ( 2 f ( x ) + x sin x - 3 g ( x ) ) d x
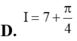
Gọi F(x) là một nguyên hàm của hàm số f(x) = xcosx thỏa mãn F(0) = 1. Khi đó phát biểu nào sau đây đúng?
A. F(x) là hàm số chẵn.
B. F(x) là hàm số lẻ.
C. Hàm số F(x) tuần hoàn với chu kì là 
.
D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.
Biết ∫ 0 π 3 x 2 d x ( x sin x + cos x ) 2 = a π b + c π 3 + d 3 với a , b , c , d ∈ ℤ Tính P = a+b+c+d
A. 9
B. 10
C. 8
D. 7
Cho hàm số y = f(x) liên tục trên [ 0 ; + ∞ ] và ∫ 0 x 2 f ( t ) d t = x sin x ( πx ) tính f(4)
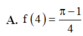
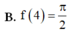
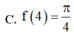
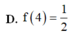
Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và y = x sin x với (0 ≤ x ≤ π) là:
A. - π 2 4
B. π 2 4
C. π 2 2
D. - π 2 2
Cho hàm số y = f ( x ) = π x 2 + 3 khi x ≥ 1 5 - x khi x < 1 . Tính I = 2 ∫ 0 π 2 f ( sin x ) cos x d x + 3 ∫ 0 1 f ( 3 - 2 x ) d x
A. I= 32 3
B. I=31
C. 71 6
D. 32
