1: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BH\left(BH+6,4\right)=6^2=36\)
=>\(BH^2+6,4BH-36=0\)
=>(BH+10)(BH-3,6)=0
=>\(\left[{}\begin{matrix}BH=-10\left(loại\right)\\BH=3,6\left(nhận\right)\end{matrix}\right.\)
=>BH=3,6(cm)
BC=BH+CH=3,6+6,4=10(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
2: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
nên ADHE là hình chữ nhật
=>AH=DE
Xét ΔBHA vuông tại H có HD là đường cao
nên \(BD\cdot BA=BH^2\)
=>\(BD=\dfrac{BH^2}{BA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC;CA^2=CH\cdot BC;AH^2=HB\cdot HC\)
=>\(BH=\dfrac{BA^2}{BC};CH=\dfrac{CA^2}{CB}\)
Xét ΔCHA vuông tại H có HE là đường cao
nên \(CE\cdot CA=CH^2\)
=>\(CE=\dfrac{CH^2}{AC}\)
\(BC\cdot BD\cdot CE=BC\cdot\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\)
\(=\dfrac{BC}{AH\cdot BC}\cdot\left(BH\cdot CH\right)^2=\dfrac{1}{AH}\cdot AH^4=AH^3=DE^3\)
3: Gọi giao điểm của NA và HD là F
Xét ΔCNH vuông tại C có \(cosCNH=\dfrac{CN}{NH}=\dfrac{NE}{NC}\)(Vì \(NC^2=NH\cdot NE\))
nên \(cos^2CNH=\dfrac{CN}{NH}\cdot\dfrac{NE}{NC}=\dfrac{NE}{NH}\)
Xét ΔNHF có AE//HF
nên \(\dfrac{AE}{HF}=\dfrac{NE}{NH}\)
=>\(cos^2CNH=\dfrac{AE}{HF}\)
Xét ΔHBM vuông tại B có BD là đường cao
nên \(HB^2=HD\cdot HM\)
=>\(\dfrac{HD}{HB}=\dfrac{HB}{HM}=cosBHM\)
=>\(cos^2BHM=\dfrac{HD}{HB}\cdot\dfrac{HB}{HM}=\dfrac{HD}{HM}=\dfrac{AE}{HM}\)
mà \(\widehat{CNH}=\widehat{BHM}\left(=\widehat{NHA}\right)\)
nên \(\dfrac{AE}{HM}=\dfrac{AE}{HF}\)
=>HM=HF
=>F trùng với M
=>N,A,M thẳng hàng






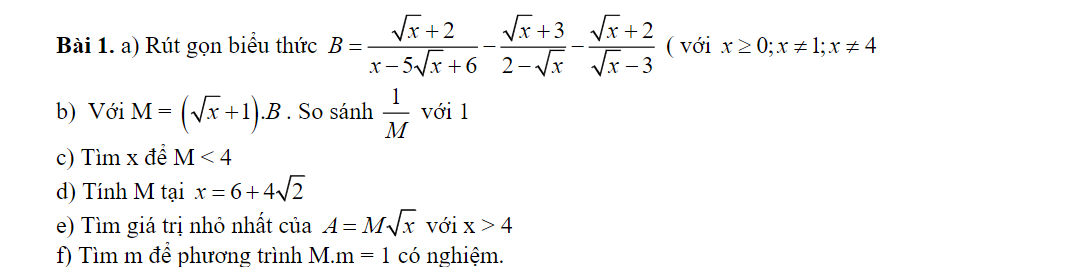 câu e và f cần giúp đỡ vs ạ
câu e và f cần giúp đỡ vs ạ 



