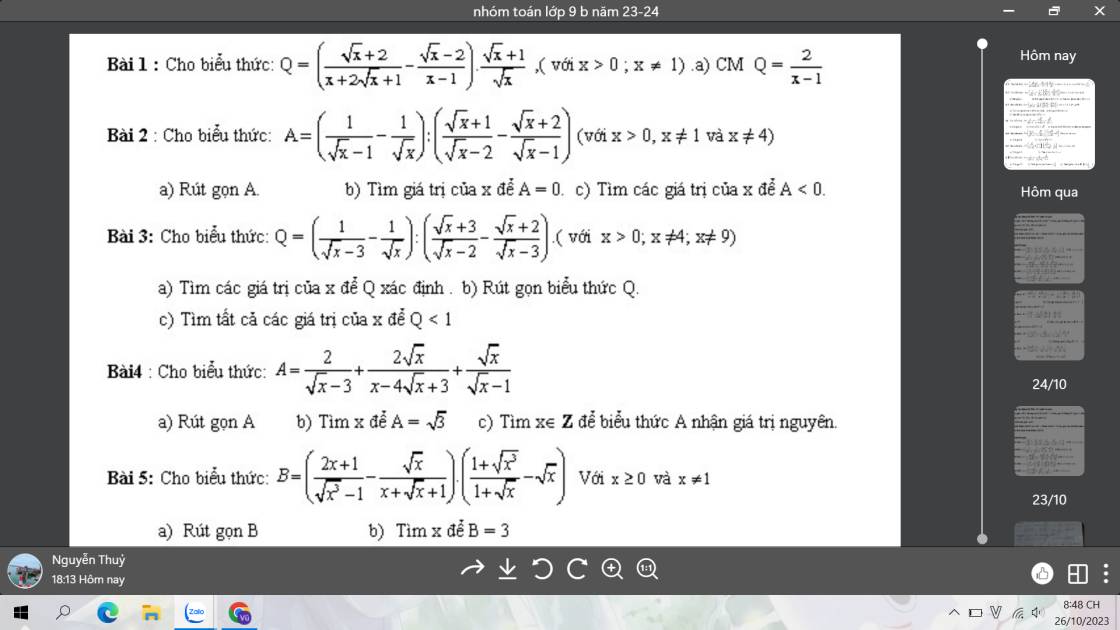
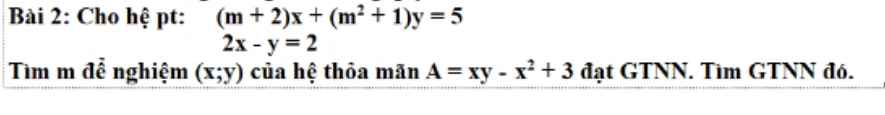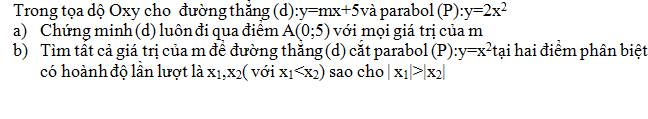Bài 2:
a. Khi $m=-5$ thì pt trở thành:
$x^2+6x+8=0$
$\Leftrightarrow (x+2)(x+4)=0\Leftrightarrow x+2=0$ hoặc $x+4=0$
$\Leftrightarrow x=-2$ hoặc $x=-4$
b.
Để pt có 2 nghiệm pb thì $\Delta=(m-1)^2-4(-m+3)>0$
$\Leftrightarrow m^2+2m-11>0(*)$
Áp dụng định lý Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=m-1$
$x_1x_2=-m+3$
Để $x_1,x_2$ trái dấu thì $x_1x_2<0\Leftrightarrow -m+3<0$
$\Leftrightarrow m> 3$
Nếu $x_1>0>x_2$ thì:
$x_1-|x_2|=3$
$\Leftrightarrow x_1-(-x_2)=3\Leftrightarrow x_1+x_2=3$
$\Leftrightarrow m-1=3\Leftrightarrow m=4$ (tm)
Nếu $x_1<0< x_2$ thì:
$x_1-|x_2|=3$
$\Leftrightarrow x_1-x_2=3$ (vô lý do $x_1<x_2$)
Vậy $m=4$
Bài IV:
1: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD\(\perp\)AE tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)EB tại C
Xét ΔEAB có
AC,BD là các đường cao
AC cắt BD tại H
Do đó: H là trực tâm của ΔEAB
=>EH\(\perp\)AB tại F
Xét tứ giác CHDE có \(\widehat{EDH}+\widehat{ECH}=90^0+90^0=180^0\)
nên CHDE là tứ giác nội tiếp đường tròn đường kính EH
tâm I là trung điểm của EH
2: Xét ΔHAD vuông tại D và ΔHBC vuông tại C có
\(\widehat{DHA}=\widehat{CHB}\)(hai góc đối đỉnh)
Do đó; ΔHAD~ΔHBC
=>\(\dfrac{HA}{HB}=\dfrac{HD}{HC}\)
=>\(HA\cdot HC=HB\cdot HD\)
Xét (O) có
\(\widehat{DBA}\) là góc nội tiếp chắn cung DA
\(\widehat{DAC}\) là góc nội tiếp chắn cung DC
\(sđ\stackrel\frown{AD}=sđ\stackrel\frown{DC}\)
Do đó: \(\widehat{DBA}=\widehat{DAC}\)
mà \(\widehat{DBA}=\widehat{DEF}\left(=90^0-\widehat{EAF}\right)\)
nên \(\widehat{DAC}=\widehat{DEF}\)(1)
Xét tứ giác AECF có \(\widehat{ACE}=\widehat{AFE}=90^0\)
nên AECF là tứ giác nội tiếp
=>\(\widehat{HCF}=\widehat{HEA}\left(2\right)\) và \(\widehat{HFC}=\widehat{HAE}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{HCF}=\widehat{HFC}\)
=>ΔHCF cân tại H