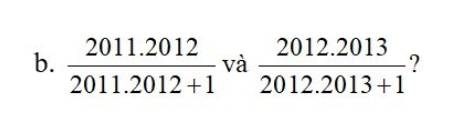\(\dfrac{2011\cdot2012}{2011\cdot2012+1}=\dfrac{2011\cdot2012+1-1}{2011\cdot2012+1}=1-\dfrac{1}{2011\cdot2012+1}\)
\(\dfrac{2012\cdot2013}{2012\cdot2013+1}=\dfrac{2012\cdot2013+1-1}{2012\cdot2013+1}=1-\dfrac{1}{2012\cdot2013+1}\)
Ta có: \(2011\cdot2012< 2012\cdot2013\)
=>\(2011\cdot2012+1< 2012\cdot2013+1\)
=>\(\dfrac{1}{2011\cdot2012+1}>\dfrac{1}{2012\cdot2013+1}\)
=>\(-\dfrac{1}{2011\cdot2012+1}< \dfrac{-1}{2012\cdot2013+1}\)
=>\(\dfrac{-1}{2011\cdot2012}+1< \dfrac{-1}{2012\cdot2013+1}+1\)
=>\(\dfrac{2011\cdot2012}{2011\cdot2012+1}< \dfrac{2012\cdot2013}{2012\cdot2013+1}\)