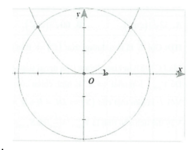

Diện tích phần giới hạn giữa đường tròn và parabol là:
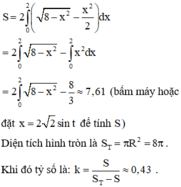
Chọn A.


Diện tích phần giới hạn giữa đường tròn và parabol là:
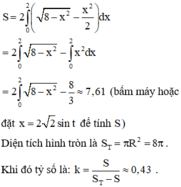
Chọn A.
Parabol y = x 2 2 chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có diện tích là S 1 và S 2 , trong đó S 1 < S 2 . Tìm tỉ số S 1 S 2
A. 3 π + 2 21 π - 2
B. 3 π + 2 9 π - 2
C. 3 π + 2 12 π
D. 9 π - 2 3 π + 2
Parabol chia hình tròn có tâm tại gốc tọa độ, bán kính 2√2 thành hai phần. Tìm tỉ số diện tích của chúng.
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , b , c = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , ( b , c ) = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x − 1 2 + y − 1 2 = 4. Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x − 1 2 + y − 1 2 = 8.
B. x − 2 2 + y − 2 2 = 8.
C. x + 2 2 + y + 2 2 = 16.
D. x − 2 2 + y − 2 2 = 16.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S tâm I 1 ; - 2 ; 1 ; bán kính R = 4 và đường thẳng d : x 2 = y - 1 - 2 = z + 1 - 1 . Mặt phẳng chứa d và cắt mặt cầu theo một đường tròn có diện tích nhỏ nhất. Hỏi trong các điểm sau điểm nào có khoảng cách đến mặt phẳng P lớn nhất.
A. O(0;0;0)
B. A 1 ; 3 5 ; - 1 4
C. (-1;-2;-3)
D. C(2;1;0)
Cho hàm số f x = x 3 − 3 x 2 − 1 có đồ thị (C) và đường thẳng d : y = x + m . Biết rằng đường thẳng (d) cắt đồ thị (C) tạo thành 2 phần hình phẳng có diện tích bằng nhau. Hỏi m thuộc khoảng nào trong các khoảng sau đây?
A. − 5 ; − 3
B. − 3 ; − 1
C. − 1 ; 1
D. 1 ; 3
Cho hàm số y = 2 x - 1 x - 2 có đồ thị (C). Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến ∆ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến ∆ của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào?
A. (26;27).
B. (29;30).
C. (27;28).
D. (28;29).
Cho hàm số y = 2 x - 1 x - 2 có đồ thị C . Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến ∆ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến ∆ của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào ?
A. 29 ; 30
B. 27 ; 28
C. 26 ; 27
D. 28 ; 29