Đáp án D.
Phương trình đường tròn tâm O có bán kính R = 2 2 là x 2 + y 2 = 8 .
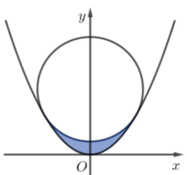
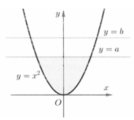
Ta có parabol và đường tròn như hình vẽ bên.
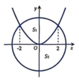
Giao điểm của parabol và đường tròn là nghiệm của hệ phương trình
x 2 + y 2 = 8 y = x 2 2 ⇔ x = ± 2 y = 2
Vì parabol và đường tròn đều đối xứng qua trục Oy nên ta có
S = 2 ∫ 0 2 8 - x 2 - x 2 2 d x .
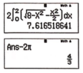
Bấm máy tính, ta được kết quả như hình bên. Ta biết S = a π + b c nên ta thao tác tiếp theo trên máy như hình bên.
Vậy ta có S = 2 π + 4 3 . Do đó ta có a = 2 , b = 4 , c = 3 ⇒ a + b + c = 9 . Chọn đáp án D.