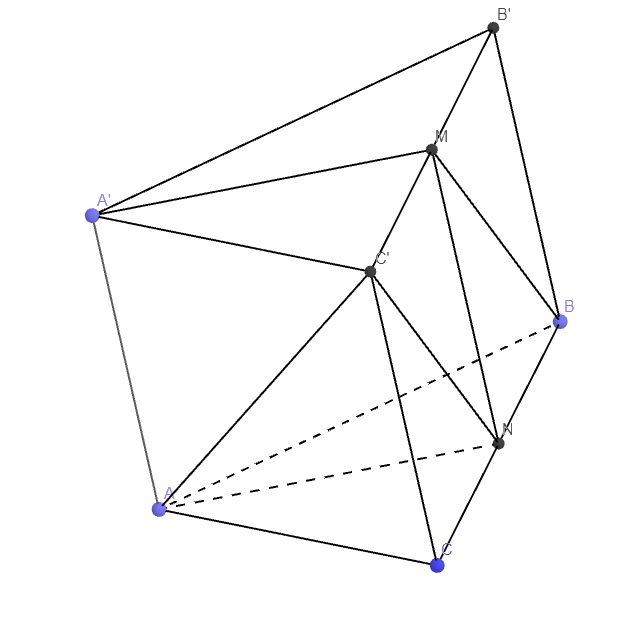
a.
Câu này em ghi sai đề, AN và AM cắt nhau tại A thì sao song song được, là AN và A'M mới đúng chứ
Giả sử N là giao điểm (AA'M) và BC
\(\Rightarrow\left\{{}\begin{matrix}\left(AA'M\right)\cap\left(ABB'A'\right)=AA'\\\left(AA'M\right)\cap\left(BCC'B'\right)=MN\\\left(ABB'A'\right)\cap\left(BCC'B'\right)=BB'\end{matrix}\right.\)
Ba mặt phẳng (AA'M), (ABB'A'), (BCC'B') cắt nhau theo 3 giao tuyến phân biệt AA', MN, BB' nên 3 giao tuyến này song song hoặc đồng quy
Mà \(AA'||BB'\Rightarrow AA'||BB'||MN\)
Lại có M là trung điểm B'C' \(\Rightarrow MN\) là đường trung bình hbh BCC'B'
\(\Rightarrow MN\) song song và bằng BB' \(\Rightarrow MN\) song song và bằng AA'
\(\Rightarrow ANMA'\) là hbh
\(\Rightarrow AN||A'M\)
b.
Do M là trung điểm B'C', N là trung điểm BC mà \(BC=B'C'\Rightarrow BN=C'M\)
\(\Rightarrow BMC'N\) là hbh (cặp cạnh đối song song và bằng nhau)
\(\Rightarrow C'N||BM\)
Lại có \(AN||A'M\) theo cm câu a
\(\Rightarrow\left(AC'N\right)||\left(BA'M\right)\)
\(\Rightarrow AC'||\left(BA'M\right)\)
c.
Gọi d là giao tuyến (AB'C') và (ABC)
Ba mặt phẳng (AB'C'), (ABC) và (BCC'B') cắt nhau theo 3 giao tuyến phân biệt là d, B'C' và BC \(\Rightarrow3\) giao tuyến song song hoặc đồng quy
Mà \(B'C'||BC\Rightarrow B'C'||BC||d\)
Vậy qua A kẻ đường thẳng d song song BC \(\Rightarrow d=\left(AB'C'\right)\cap\left(ABC\right)\)