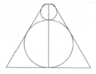
Người ta sản xuất một vật lưu niệm (N) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết diện qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong (N) có hai khối cầu ngũ sắc với bán kính lần lượt là R = 3 cm, r = 1 cm tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của (N), đồng thời hai khối cầu lần lượt tiếp xúc với hai mặt đáy của (N). Tính thể tích vật lưu niệm đó
A. 458 π 6 ( c m 3 )
B. 81 π cm 3
C. 72 π cm 3
D. 728 π 9 c m 3
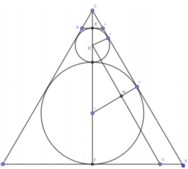
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.