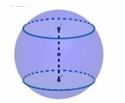
Có một khối cầu bằng gỗ bán kính R = 10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng 1 2 R đối xứng nhau qua tâm của khối cầu, một người thợ mộc đục xuyên tâm của khối cầu gỗ. Người thợ mộc đã đục bỏ đi phần hình hộp chữ nhật có trục của nó trùng với trục hình cầu và có hai mặt lần lượt nằm trên hai mặt phẳng chứa hai đáy của chỏm cầu; hai mặt này là hai hình vuông có đường chéo bằng R (tham khảo hình vẽ bên).
Tính thể tích V của phần còn lại của khối cầu (làm tròn đến chữ số thập phân thứ ba)

A. V = 3215 , 023 c m 3 .
B. V = 3322 , 765 c m 3 .
C. V = 3268 , 894 c m 3 .
D. V = 3161 , 152 c m 3 .
Đáp án A.
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.