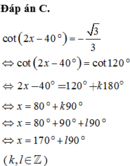Các câu hỏi tương tự
Cho
a
log
2
5
. Ta phân tích được
log
4
1000
m
a
+
n
k
m
,
n
,
k
∈
ℤ
. Tính
m
2
+...
Đọc tiếp
Cho a = log 2 5 . Ta phân tích được log 4 1000 = m a + n k m , n , k ∈ ℤ . Tính m 2 + n 2 + k 2
A. 13
B. 10
C. 22
D. 14
Giả sử phương trình
l
o
g
2
2
2
x
-
3
l
o
g
2
x
-
2
0
có một nghiệm dạng
x
2
a
+
b
c
với
a
,...
Đọc tiếp
Giả sử phương trình l o g 2 2 2 x - 3 l o g 2 x - 2 = 0 có một nghiệm dạng x = 2 a + b c với a , b , c ∈ ℤ + và b < 20 . Tính tổng a + b + c 2
A. 10
B. 11
C. 18
D. 27
Biện luận theo k số nghiệm của phương trình:
a) ( x - 1 ) 2 = 2|x − k|
b) ( x + 1 ) 2 .(2 − x) = k
Xét phương trình
2
a
x
-
x
2
3
x
;
a
∈
ℤ
ngoài nghiệm x0 ra thì: A. Có nghiệm
x
a
-
log
2...
Đọc tiếp
Xét phương trình 2 a x - x 2 = 3 x ; a ∈ ℤ ngoài nghiệm x=0 ra thì:
A. Có nghiệm x = a - log 2 3
B. Có nghiệm x = a - log 2 1 3
C. Có nghiệm x = a - log 3 2
D. Không có nghiệm khác
Biện luận theo k số nghiệm của phương trình: x - 1 2 = 2|x − k|
Biện luận theo k số nghiệm của phương trình: x + 1 2 .(2 − x) = k
Cho hàm số
f
x
a
x
4
+
2
b
x
3
-
3
c
x
2
-
4
d
x
+
5
h
a
,
b
,
c
,
d
,...
Đọc tiếp
Cho hàm số f x = a x 4 + 2 b x 3 - 3 c x 2 - 4 d x + 5 h a , b , c , d , h ∈ ℤ . Hàm số y=f'(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)=5h có số phần tử bằng:
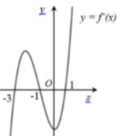
A. 3
B. 4
C. 2
D. 1
Phương trình
4
x
3
-
3
x
2
2
có bao nhiêu nghiệm? Gọi số nghiệm là k. Xác định k.
Đọc tiếp
Phương trình 4 x 3 - 3 x = 2 2 có bao nhiêu nghiệm? Gọi số nghiệm là k. Xác định k.
![]()
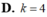
Cho hàm số
f
(
x
)
3
x
-
4
+
(
x
+
1
)
.
2
7
-
x
-
6
x
+
3
. Giả sử
m
0
a
b...
Đọc tiếp
Cho hàm số f ( x ) = 3 x - 4 + ( x + 1 ) . 2 7 - x - 6 x + 3 . Giả sử m 0 = a b a , b ∈ ℤ , a b l à p h â n s ố t ố i g i ả n là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 - 4 6 x - 9 x 2 + 2 m - 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. 11
B. 7
C. -1
D. 9
Số tiền mà My để dành hằng ngày là x (đơn vị nghìn đồng, với x 0,
x
∈
ℤ
) biết x là nghiệm của phương trình
log
3
(
x
-
2
)
+
log
3
(
x
-
4
)
2
0
. Tính tổng số tiền My để dành được ...
Đọc tiếp
Số tiền mà My để dành hằng ngày là x (đơn vị nghìn đồng, với x > 0, x ∈ ℤ ) biết x là nghiệm của phương trình log 3 ( x - 2 ) + log 3 ( x - 4 ) 2 = 0 . Tính tổng số tiền My để dành được trong một tuần (7 ngày).
A. 35 nghìn đồng.
B. 14 nghìn đồng.
C. 21 nghìn đồng.
D. 28 nghìn đồng.