Tổng ba góc trong 1 tam giác bằng 180 độ
| GT | ΔABC |
| KL | góc A+góc B+góc C=180 độ |
Tổng ba góc trong 1 tam giác bằng 180 độ
| GT | ΔABC |
| KL | góc A+góc B+góc C=180 độ |
Nêu định lý về tổng các góc trong 1 tam giác vẽ hình ghi giả thiết kết luận của định lí đó
A) Hãy viết định lí nói về 1 đường thẳng vuông góc với một trong hai đường thẳng song song
B) Vẽ hình minh họa định lí đó và viết giả thiết,kết luận bằng kí hiệu
chỉ cần ghi định lí,giả thiết,kết luận thôi!
Vẽ hình và viết giả thiết , kết luận của định lí sau : << Tổng ba góc của một hình tam giác là 180 độ >>
2 : Phát biểu tính chất : " Hai tia phân giác của 2 góc kề bù tạo thành góc vuông " thành định lí dạng : Nếu.... thì
rồi vẽ hình và ghi Giả thiết , kết luận của định lí
Chứng minh định lí và phát biểu
Vẽ hình, ghi giả thiết, kết luận và chứng minh định lí " Nếu 1 duong thẳng cắt hai đường thẳng song song thì hai tia phân giác của một cặp góc trong cùng phía vuông góc với nhau. ( giúp mk vs, mk đã vẽ đc hình và ghi giả thiết kết luận rùi nhg ko bt chứng minh ntn hết, giải đc mk sẽ cho 3 k ah, nhanh nhek)
Bài 1: Vẽ hình,ghi giả thiết, kết luận và CM định lí: Cho 2 góc kề nhau và phụ nhau thì 2 tia phân giác của chúng tạo thành góc 45°
vẽ hình và ghi giả thiết kết luận cho định lí sau :
tia phân giác của góc thì tạo với 2 cạnh của góc 2 góc bằng nhau
Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
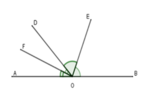
A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF
B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA
C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF
D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OB ⊥ OF
Vẽ hình ghi giả thiết và kết luận chứng minh định lí
Nếu hai đường thẳng song song thì các tia phân giác của mỗi cặp góc đồng vị được tạo bởi một đường thẳng cắt hai đường thẳng đó song song với nhau