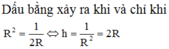Các câu hỏi tương tự
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu? A.
r
V
π
2...
Đọc tiếp
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?
A. r = V π 2 3
B. r = V 3
C. r = V 2 π 3
D. r = V 2 3
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là: A.
h
R
1
B.
h
R
2
C.
h
R
2
D.
h
R
1
2
Đọc tiếp
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
A. h R = 1
B. h R = 2
C. h R = 2
D. h R = 1 2
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon nhỏ nhất. Muốn thể tích khối trụ là V mà diện tích toàn phần của hình trụ nhỏ nhất thì bán kính R của đường tròn đáy khối trụ bằng?
Đọc tiếp
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon nhỏ nhất. Muốn thể tích khối trụ là V mà diện tích toàn phần của hình trụ nhỏ nhất thì bán kính R của đường tròn đáy khối trụ bằng?
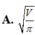
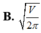
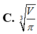
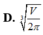
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon là nhỏ nhất. Muốn thể tích khối trụ bằng V mà diện tích toàn phần của hình trụ là nhỏ nhất thì bán kính R của mặt tròn đáy khối trụ bằng?
Đọc tiếp
Khi thiết kế vỏ lon sữa hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí làm vỏ lon là nhỏ nhất. Muốn thể tích khối trụ bằng V mà diện tích toàn phần của hình trụ là nhỏ nhất thì bán kính R của mặt tròn đáy khối trụ bằng?
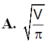
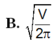
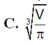
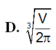
Cho hình trụ có bán kính đường tròn đáy là R, độ dài đường cao h. Kí hiệu Stp là diện tích toàn phần của hình trụ và V là thể tích khối trụ. Trong các mệnh đề sau, mệnh đề nào đúng? A.
V
1
3
π
R
2
h
B. ...
Đọc tiếp
Cho hình trụ có bán kính đường tròn đáy là R, độ dài đường cao h. Kí hiệu Stp là diện tích toàn phần của hình trụ và V là thể tích khối trụ. Trong các mệnh đề sau, mệnh đề nào đúng?
A. V = 1 3 π R 2 h
B. S t p = π R h
C. S t p = 2 π R h + π R 2 h
D. S t p = 2 π R ( h + R )
Một khối trụ có thể tích bằng
25
π
.Nếu chiều cao hình trụ tăng lên năm lần và giữa nguyên bán kính đáy thì được một hình trụ mới có diện tích xung quanh bằng
25
π
. Tính bán kính đáy r của hình trụ ban đầu. A. r15 B. r5 C. r10 D. r2
Đọc tiếp
Một khối trụ có thể tích bằng 25 π .Nếu chiều cao hình trụ tăng lên năm lần và giữa nguyên bán kính đáy thì được một hình trụ mới có diện tích xung quanh bằng 25 π . Tính bán kính đáy r của hình trụ ban đầu.
A. r=15
B. r=5
C. r=10
D. r=2
Một nhà máy sản xuất nước ngọt cần làm các lon dựng dạng hình trụ với thể tích đựng được là V. Biết rằng diện tích toàn phần nhỏ nhất thì tiết kiệm chi phí nhất. Tính bán kính của lon để tiết kiệm chi phí nhất.
Đọc tiếp
Một nhà máy sản xuất nước ngọt cần làm các lon dựng dạng hình trụ với thể tích đựng được là V. Biết rằng diện tích toàn phần nhỏ nhất thì tiết kiệm chi phí nhất. Tính bán kính của lon để tiết kiệm chi phí nhất.
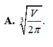
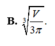
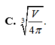
Cho hình nón (N) có bán kính đáy r20(cm), chiều cao h60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
Đọc tiếp
Cho hình nón (N) có bán kính đáy r=20(cm), chiều cao h=60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
![]()
![]()
![]()
![]()
Cho một hình trụ có bán kính đáy R, chiều cao h, thể tích
V
1
và một hình nón có đáy trùng với đáy của một hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (xem hình) và thể tích
V
2
. Hệ thức giữa
V
1
và
V
2
là:A.
V...
Đọc tiếp
Cho một hình trụ có bán kính đáy R, chiều cao h, thể tích V 1 và một hình nón có đáy trùng với đáy của một hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (xem hình) và thể tích V 2 . Hệ thức giữa V 1 và V 2 là:
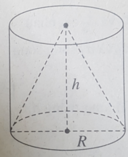
A. V 1 = 2 V 2 B. V 1 = 3 V 2
C. V 2 = 3 V 1 D. V 2 = V 1