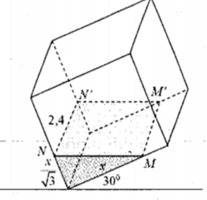
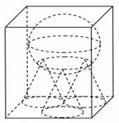
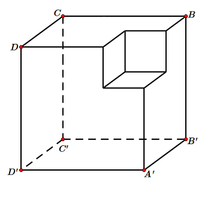
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2
Đáp án B
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC’ và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa mãn yêu cầu bài toán.
Ta có d I ; A ' B ' C ' D ' = d I ; B C C ' B ' = d I ; D C C ' D '
Suy ra I thuộc đoạn thẳng C’M và mặt cầu tâm I cần tìm đi qua điểm M.
Đặt d I ; D C C ' D ' = a , ta có IC' = a 3 mà A C ' = 3 3 , A M = 3
Suy ra I M = 2 3 - a 3 mặt khác d I ; D C C ' D ' = I M ⇔ a = 2 3 - a 3 ⇒ a = 3 - 3 3