Đáp án D
V = S d . h = a 2 . a = a 3 .
Đáp án D
V = S d . h = a 2 . a = a 3 .
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó.
A. π a 3 6
B. 4 π a 3 3
C. π 2 a 3 3
D. π 3 a 3 2
Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a 3
A. V= 3 3 a 3
B. V= 27 a 3
C. V= a 3
D. V= 3 a 3
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Tính thể tích V của khối chóp D ' . A B C D .
A. V = a 3 4
B. V = a 3 6
C. V = a 3 3
D. V = a 3
Một khối trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính theo a thể tích V của khối trụ đó
A. V = π a 3 2
B. V = π a 3 4
C. V = π a 3
D. V = 2 π a 3
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A′BD có thể tích bằng
A. 2 3 πa 3 27
B. 3 πa 3 8
C. 3 a 3 27
D. πa 3 6
Người ta gọt một khối lập phương gỗ đê lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt; khối lập phương). Biết các cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó:
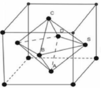
A. a 3 4
B. a 3 6
C. a 3 12
D. a 3 8
Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính thể tích của khối trụ đó.
A. πa 3
B. 2 πa 3
C. πa 3 2
D. πa 3 4
Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính thể tích của khối trụ đó.
A. π a 3
B. 2 π a 3
C. π a 3 2
D. π a 3 4
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
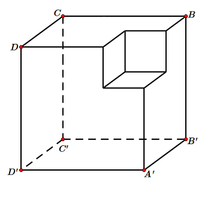
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2