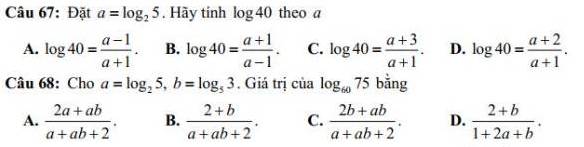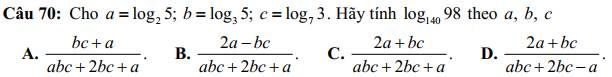Câu 67:
\(\log_{ }40=\dfrac{\log_240}{\log_210}=\dfrac{\log_25+\log_22^3}{\log_25+\log_22}=\dfrac{a+3}{a+1}\)
-> Chọn C
Câu 68::
\(\log_{60}75=\dfrac{\log_275}{\log_260}=\dfrac{\log_23+\log_25^2}{\log_22^2+\log_23+\log_25}\)
\(=\dfrac{\dfrac{\log_53}{\log_52}+2\log_25}{2+\dfrac{\log_53}{\log_52}+\log_25}=\dfrac{\log_25\cdot\log_53+2\log_25}{2+\log_25\cdot\log_53+\log_25}=\dfrac{ab+2a}{2+ab+a}\)
-> Chọn A
Câu 70:
\(\log_{140}98=\dfrac{\log_398}{\log_3140}=\dfrac{\log_349+\log_32}{\log_32^2+\log_35+\log_37}=\dfrac{2\log_37+\log_32}{2\log_32+\log_35+log_37}\)
\(=\dfrac{2\cdot\dfrac{1}{\log_73}+\dfrac{\log_52}{\log_53}}{2\cdot\dfrac{\log_52}{\log_53}+\log_35+\dfrac{1}{\log_73}}=\dfrac{2\cdot\dfrac{1}{\log_73}+\dfrac{\log_35}{\log_25}}{2\cdot\dfrac{\log_35}{\log_25}+\log_35+\dfrac{1}{\log_73}}\)
\(=\dfrac{2\cdot\dfrac{1}{c}+\dfrac{b}{a}}{2\cdot\dfrac{b}{a}+b+\dfrac{1}{c}}=\dfrac{2a+bc}{abc+2bc+a}\)
-> Chọn C