Bài 7:
a) Ta có: x:2=y:5
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=3\\\dfrac{y}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=15\end{matrix}\right.\)
c) Ta có: x:2=y:7
nên \(\dfrac{x}{2}=\dfrac{y}{7}\)
mà x+y=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{7}=\dfrac{x+y}{2+7}=\dfrac{18}{9}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=2\\\dfrac{y}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=14\end{matrix}\right.\)
Bài 8:
a) Ta có: \(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\)
nên \(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}\)
mà 2a+3b-c=50
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2a}{6}=\dfrac{3b}{24}=\dfrac{c}{5}=\dfrac{2a+3b-c}{6+24-5}=\dfrac{50}{25}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=2\\\dfrac{b}{8}=2\\\dfrac{c}{5}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=16\\c=10\end{matrix}\right.\)
Bài 8:
b) Ta có: \(\dfrac{x}{10}=\dfrac{y}{5}\)
nên \(\dfrac{x}{20}=\dfrac{y}{10}\)(1)
Ta có: \(\dfrac{y}{2}=\dfrac{z}{3}\)
nên \(\dfrac{y}{10}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
\(\Leftrightarrow\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}\)
mà 2x-3y+4z=330
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{40}=\dfrac{3y}{30}=\dfrac{4z}{60}=\dfrac{2x-3y+4z}{40-30+60}=\dfrac{330}{70}=\dfrac{33}{7}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{20}=\dfrac{33}{7}\\\dfrac{y}{10}=\dfrac{33}{7}\\\dfrac{z}{15}=\dfrac{33}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{660}{7}\\y=\dfrac{330}{7}\\z=\dfrac{495}{7}\end{matrix}\right.\)
c) Ta có: 3x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
hay \(\dfrac{x}{10}=\dfrac{y}{15}\)(1)
Ta có: 7x=5z
nên \(\dfrac{x}{5}=\dfrac{z}{7}\)
hay \(\dfrac{x}{10}=\dfrac{z}{14}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x-y+z}{10-15+14}=\dfrac{32}{9}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{10}=\dfrac{32}{9}\\\dfrac{y}{15}=\dfrac{32}{9}\\\dfrac{z}{14}=\dfrac{32}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{320}{9}\\y=\dfrac{480}{9}=\dfrac{160}{3}\\z=\dfrac{448}{9}\end{matrix}\right.\)

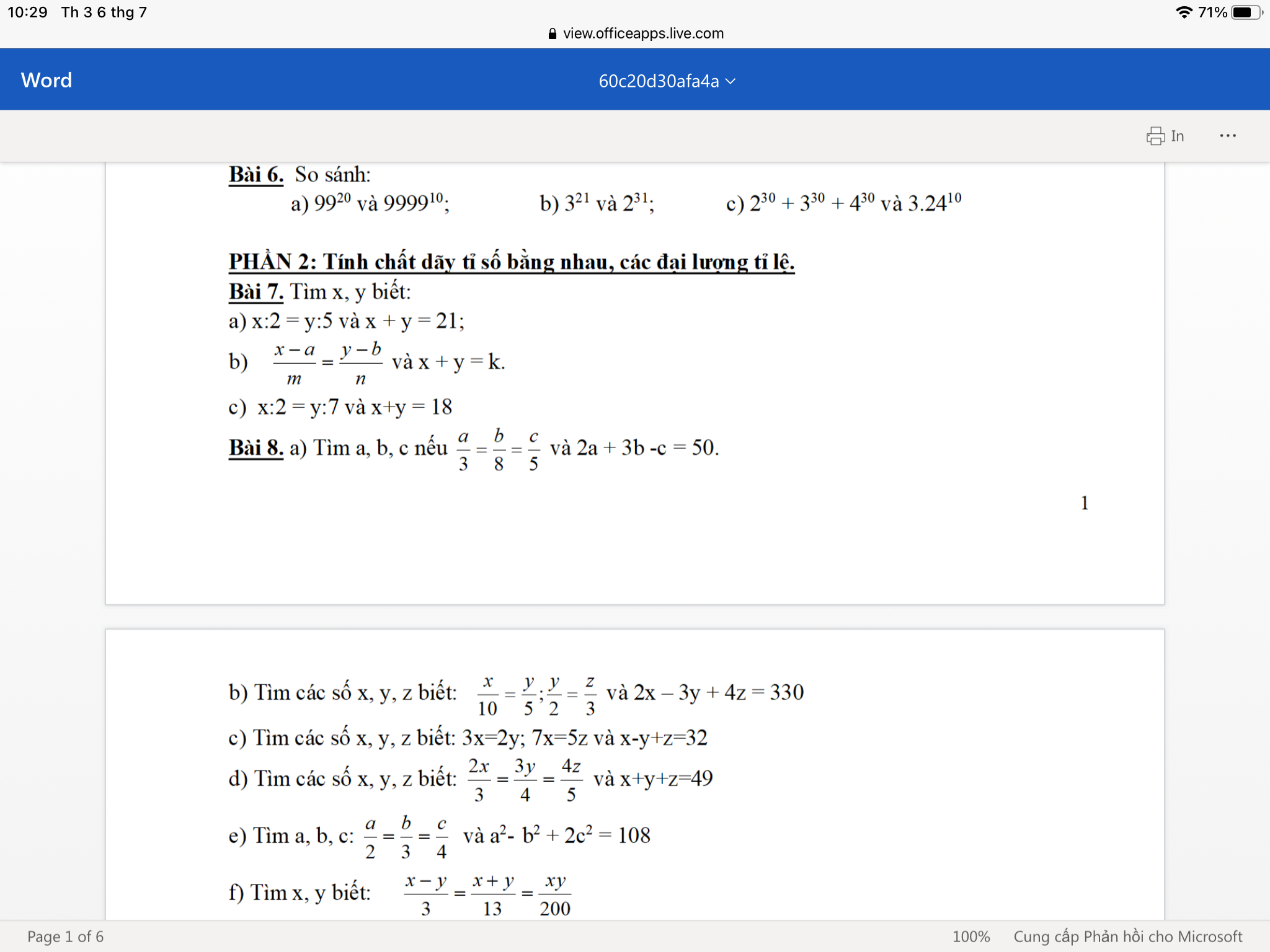






 Mọi người ơi làm giúp mình nha (làm 1 câu cũng được, 2 câu cũng được, mình tick tất nha)
Mọi người ơi làm giúp mình nha (làm 1 câu cũng được, 2 câu cũng được, mình tick tất nha)


