2.
Xét khai triển:
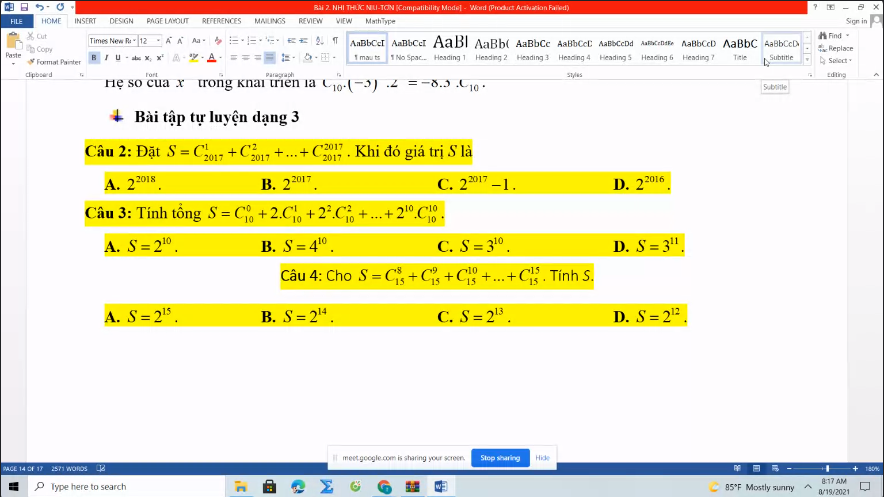
\(\left(1+x\right)^{2017}=C_{2017}^0+C_{2017}^1.x+C_{2017}^2x^2+...+C_{2017}^{2017}x^{2017}\)
Cho \(x=1\) ta được:
\(2^{2017}=C_{2017}^0+C_{2017}^1+...+C_{2017}^{2017}\)
\(\Rightarrow C_{2017}^1+C_{2017}^2+...+C_{2017}^{2017}=2^{2017}-C_{2017}^0=2^{2017}-1\)
3.
Xét khai triển:
\(\left(1+x\right)^{10}=C_{10}^0+C_{10}^1x+...+C_{10}^{10}x^{10}\)
Thay \(x=2\) ta được:
\(3^{10}=C_{10}^0+2C_{10}^1+2^2C_{10}^2+...+2^{10}C_{10}^{10}\)
\(\Rightarrow S=3^{10}\)
4.
Xét khai triển:
\(\left(1+x\right)^{15}=C_{15}^0+C_{15}^1x+...+C_{15}^{15}x^{15}\)
Thay \(x=1\) ta được:
\(2^{15}=C_{15}^0+C_{15}^1+...+C_{15}^{15}\)
Mặt khác, áp dụng công thức: \(C_n^k=C_n^{n-k}\) ta có:
\(C_{15}^0=C_{15}^{15}\)
\(C_{15}^1=C_{15}^{14}\)
...
\(C_{15}^7=C_{15}^8\)
Cộng vế:
\(C_{15}^0+C_{15}^1+...+C_{15}^7=C_{15}^8+C_{15}^9+...+C_{15}^{15}\)
\(\Rightarrow C_{15}^0+C_{15}^1+...+C_{15}^{15}=2\left(C_{15}^8+C_{15}^9+...+C_{15}^{15}\right)\)
\(\Rightarrow2S=2^{15}\)
\(\Rightarrow S=2^{14}\)
5.
Xét khai triển:
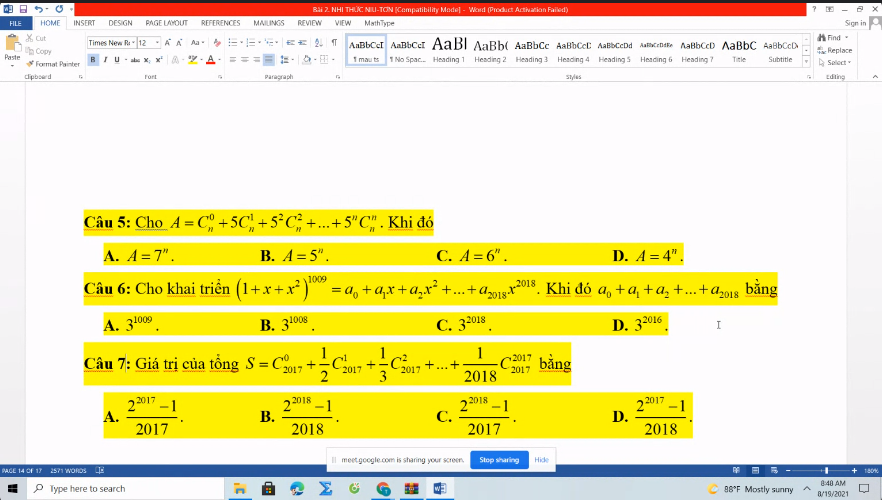
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^nC_n^n\)
Thay \(x=5\) ta được:
\(6^n=C_n^0+5C_n^1+...+5^nC_n^n\)
\(\Rightarrow A=6^n\)
6.
\(\left(1+x+x^2\right)^{1009}=a_0+a_1x+...+a_{2018}x^{2018}\)
Thay \(x=1\) ta được:
\(3^{1009}=a_0+a_1+...+a_{2018}\)
7.
Xét khai triển:
\(\left(1+x\right)^{2017}=C_{2017}^0+C_{2017}^1x+...+C_{2017}^{2017}x^{2017}\)
Lấy tích phân 2 vế:
\(\int\limits^1_0\left(1+x\right)^{2017}dx=\int\limits^1_0\left(C_{2017}^0+C_{2017}^1x+...+C_{2017}^{2017}x^{2017}\right)\)
\(\Rightarrow\dfrac{2^{2018}-1}{2018}=C_{2017}^0+\dfrac{1}{2}C_{2017}^1+...+\dfrac{1}{2018}C_{2017}^{2017}\)