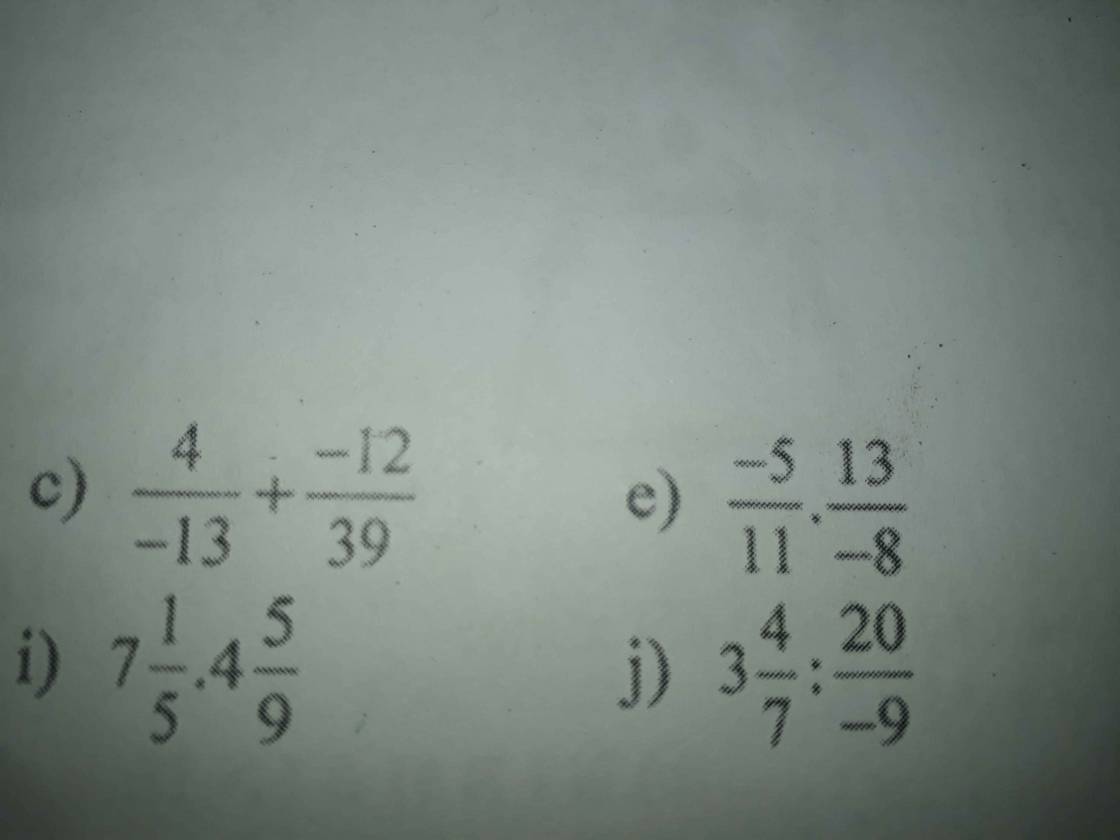\(\dfrac{B}{A}=\dfrac{1+\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2022}}\)
\(=\dfrac{\dfrac{2022}{2022}+\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}\)
=2022




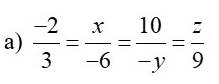 giúp mình với mọi người
giúp mình với mọi người