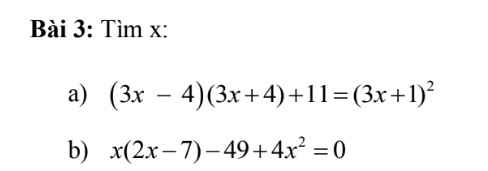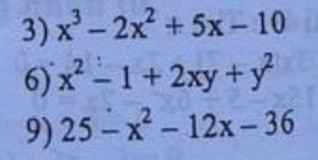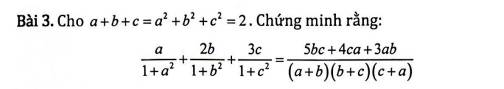Bài 6:
a: Xét ΔABC có FE//BC
nên \(\dfrac{FE}{BC}=\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
=>\(\dfrac{FE}{12}=\dfrac{AF}{6}=\dfrac{3}{9}=\dfrac{1}{3}\)
=>\(FE=\dfrac{12}{3}=4\left(cm\right);AF=\dfrac{6}{3}=2\left(cm\right)\)
b: Xét ΔABI có ED//BI
nên \(\dfrac{ED}{BI}=\dfrac{AD}{AI}\left(1\right)\)
Xét ΔACI có DF//IC
nên \(\dfrac{DF}{IC}=\dfrac{AD}{AI}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{ED}{BI}=\dfrac{DF}{IC}\)
mà BI=IC(I là trung điểm của BC)
nên DE=DF
=>D là trung điểm của EF
Bài 7:
a: Xét ΔABC có AP là phân giác
nên \(\dfrac{PB}{AB}=\dfrac{PC}{AC}\)
=>\(\dfrac{PB}{6}=\dfrac{3}{9}=\dfrac{1}{3}\)
=>PB=6/3=2(cm)
BC=BP+CP
=2+3
=5(cm)
b: Xét ΔCAB có AP//BE
nên \(\dfrac{AP}{BE}=\dfrac{CP}{CB}\)
Xét ΔBFC có AP//FC
nên \(\dfrac{AP}{FC}=\dfrac{BP}{BC}\)
\(\dfrac{AP}{BE}+\dfrac{AP}{FC}=\dfrac{BP}{BC}+\dfrac{CP}{BC}=1\)
=>\(\dfrac{1}{BE}+\dfrac{1}{FC}=\dfrac{1}{AP}\)