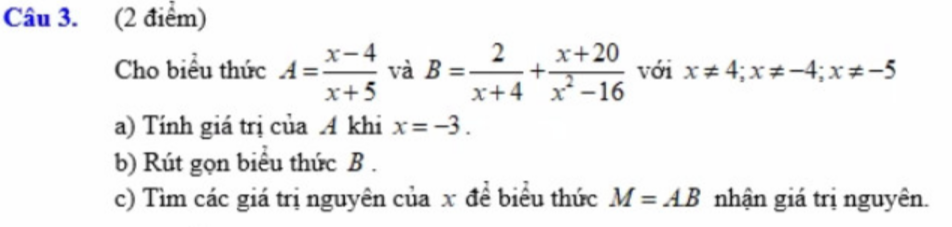Question

Mọi người giúp em với 

Answer 1

- Bạn thi xong rồi mình chỉ.

Answer 2

\(Câu3\)

 \(a^3+1+1\ge^{AM-GM}3\sqrt[3]{c^3.1.1}=3a\) \(\left(1\right)\) 

\(b^3+1+1\ge^{AM-GM}3\sqrt[3]{b^3.1.1}=3b\) \(\left(2\right)\) 

\(c^3+1+1\ge^{AM-GM}3\sqrt[3]{c^3.1.1}=3c\) \(\left(3\right)\)

\(Cộng\) \(\left(1\right),\left(2\right),\left(3\right)\) \(ta\) \(được\) :

\(a^3+b^3+c^3+1+1+1+1+1+1\ge3\left(a+b+c\right)\)

⇔\(a^3+b^3+c^3\ge3.3-6\) \(=3\) \(vì\) \(a+b+c=3\) 

\(Đẳng\) \(thức\) \(xảy\) \(ra\)⇔ \(a=b=c=1\)

 

Answer 3

Bài 1: 

a) Đặt n²+7n+1=k² 

=>4n²+28n+4=4k²

=>(4n²+28n+49)-4k²=45

=>(2n+7)²-4k²=45

=>(2n-2k+7)(2n+2k+7)=45

*Vì 2n+2k+7>2n-2k+7>0 và chúng là những số tự nhiên nên ta có thể viết: (2n-2k+7)(2n+2k+7)=1.45 hoặc 3.15

=>2n-2k+7=1 ; 2n+2k+7=45 hay 2n-2k+7=3 ; 2n+2k+7=15

=> n=1 thì k=3 ; n=8 thì k=121

Answer 4

Câu 2 \(a+b\ge4=>ab\le4\)

\(a+b+\dfrac{1}{a}+\dfrac{1}{b}\ge4+\dfrac{a+b}{ab}=4+1=5\)

Answer 5

Bài 2:

b) x²+4x=y⁴+4y ⇔ x²+4x+1=y⁴+4y+1 ⇔(2x+1)²=(2y²+1)²

⇔(2y²+1)²-(2x+1)² =0 ⇔(2y²-2x)(2y²+2x+2)=0

⇔2y²-2x=0 hay 2y²+2x+2=0

⇔y²-x=0 hay y²+x+2=0

⇔x=y=0 hay x=y=1.

Answer 6

Bài 2: (chỉnh lại)

b) x²+4x=y⁴+4y ⇔ x²+4x+4=y⁴+4y+4 ⇔(x+2)²=(y²+2)²

⇔(y²+2)²-(x+2)² =0 ⇔(y²-x)(y²+x+4)=0

⇔y²-x=0 hay y²+x+4=0

⇔y²-x=0 hay y²+x+4=0

Bài 2:

b) x²+4x=y⁴+4y ⇔ x²+4x+1=y⁴+4y+1 ⇔(2x+1)²=(2y²+1)²

⇔(2y²+1)²-(2x+1)² =0 ⇔(2y²-2x)(2y²+2x+2)=0

⇔2y²-2x=0 hay 2y²+2x+2=0

⇔y²-x=0 hay y²+x+2=0

⇔y=\(\sqrt{x}\)