-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Mọi người giúp em với ạ, nếu đc thù em xin cả cách giải, em đang cần gấp lắm ạ, cảm ơn mọi người nhiều


Cần gấp ạ, xin mọi người giúp em vs ạ. Em cảm ơn mọi người. Nếu đc em xin cả cách giải ạ


Nhờ mọi người giúp vs, em đg cần gấp ạ, cho em xin cả cách giải với ạ. Em cảm ơn mọ người


mọi người ơi giải giúp em phương trình này với ạ
3x(2-x)-5 = 1-(3x ngũ 2 + 2)
giải chi tiết giúp em với ạ cảm ơn mọi người nhiều ạ
Cần mọi người giúp ạ, nếu đc thì cho em xin cả cách giải, em cảm ơn ạ (°v°)


Mong mọi người giải giúp em với ạ em cảm ơn nhiều lắm ạ
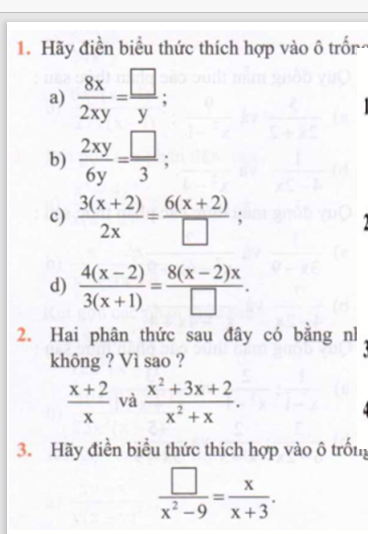 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giúp em bài này với ạ!!! Em cảm ơn mọi người nhiều ạ
