mọi người giúp em với ạ
Bài 3:
a: Xét ΔDEB vuông tại E và ΔDFC vuông tại F có
DB=DC
\(\widehat{DBE}=\widehat{DCF}\)
Do đó: ΔDEB=ΔDFC
b: ΔDEB=ΔDFC
=>DE=DF
Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
DE=DF
Do đó: ΔAED=ΔAFD
=>AE=AF
Bài 4:
a: Xét ΔDBA vuông tại D và ΔDEC vuông tại D có
DB=DE
DA=DC
Do đó: ΔDBA=ΔDEC
=>AB=CE
b: ΔDBA=ΔDEC
=>\(\widehat{DBA}=\widehat{DEC}\)
=>\(\widehat{DBA}+\widehat{DCE}=90^0\)
=>CF\(\perp\)AB tại F
Đúng 1
Bình luận (0)
a) Xét \(\Delta DEB\) vuông và \(\Delta DFC\) vuông có:
\(\widehat{B}\) = \(\widehat{C}\) (gt)
BD = DC (gt)
Do đó:\(\Delta DEB\) = \(\Delta DFC\) ( cạnh huyền - góc nhọn)
(mik chỉ bít m câu a thui ạ :) mong bn thông cảm nhé!
Đúng 0
Bình luận (0)
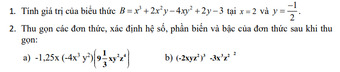
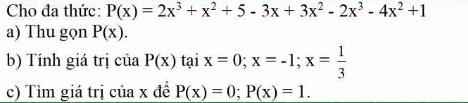
mng giúp em với ạ.Em rất cảm ơn mọi người ạ
