mọi người giúp em với ạ
Bài 6:
Gọi số tờ giấy bạc loại 10000 đồng; 20000 đồng; 50000 đồng lần lượt là a(tờ), b(tờ), c(tờ)
(Điều kiện: \(a,b,c\in Z^+\))
Tổng số tiền của mỗi mệnh giá là như nhau nên ta có:
10000a=20000b=50000c
=>a=2b=5c
=>\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{2}\)
Có tổng cộng là 85 tờ giấy bạc nên a+b+c=85
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{2}=\dfrac{a+b+c}{10+5+2}=\dfrac{85}{17}=5\)
=>\(\left\{{}\begin{matrix}a=5\cdot10=50\\b=5\cdot5=25\\c=5\cdot2=10\end{matrix}\right.\left(nhận\right)\)
vậy: Có 50 tờ 10000 đồng; 25 tờ 20000 đồng; 10 tờ 50000 đồng
Bài 5: Gọi độ dài quãng đường AB là x(km/h)
(Điều kiện: x>0)
Thời gian ô tô thứ nhất đi từ A đến B là \(\dfrac{x}{45}\left(giờ\right)\)
Thời gian ô tô thứ hai đi từ A đến B là \(\dfrac{x}{60}\left(giờ\right)\)
Ô tô thứ hai đến trước ô tô thứ nhất 40p=2/3 giờ nên ta có:
\(\dfrac{x}{45}-\dfrac{x}{60}=\dfrac{2}{3}\)
=>\(\dfrac{4x}{180}-\dfrac{3x}{180}=\dfrac{2}{3}\)
=>\(\dfrac{x}{180}=\dfrac{2}{3}\)
=>\(x=180\cdot\dfrac{2}{3}=120\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 120km
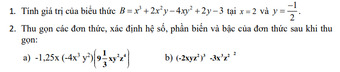
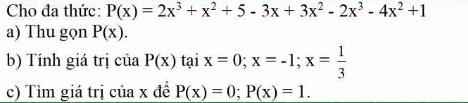
mng giúp em với ạ.Em rất cảm ơn mọi người ạ
