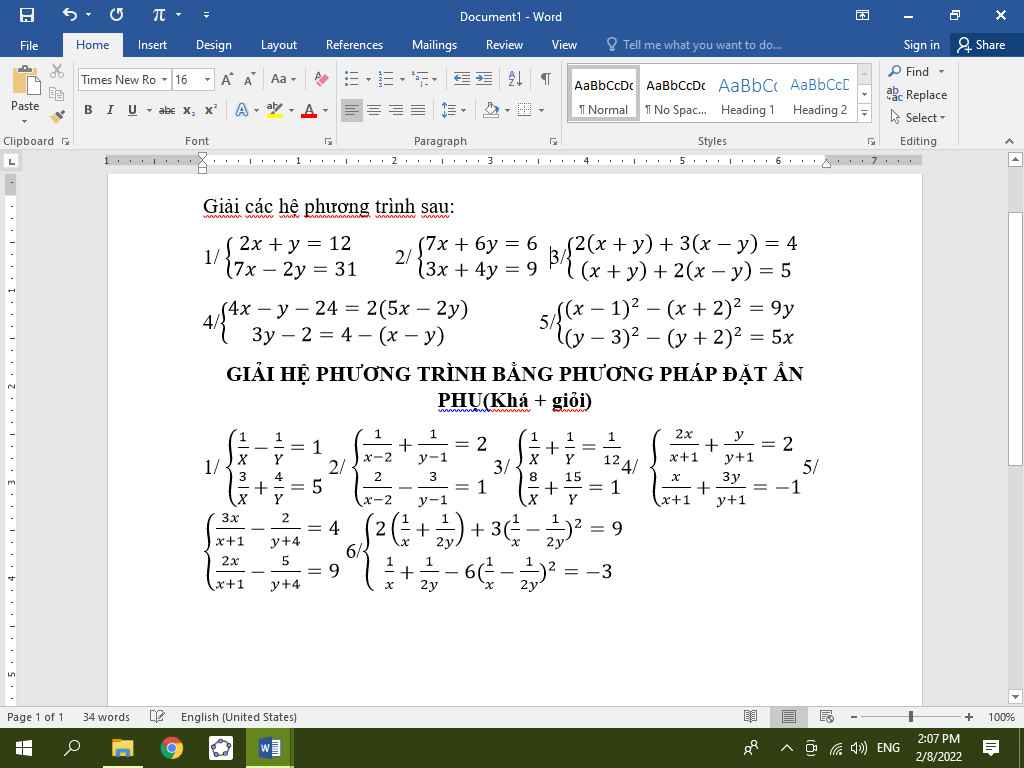
\(2/\)
\(a,\) Rút gọn
\(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\left(dkxd:x\ne4,x\ge0\right)\)
\(=\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+\left(\sqrt{x}+2\right)+\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(b,\) Để \(A>1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-2}>1\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-2}-1>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-\left(\sqrt{x}-2\right)}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+2>0\)
\(\Leftrightarrow2>0\left(LD\right)\)
Vậy với mọi giá trị x thì \(A>1\)
\(3/\)
\(x^2-2\left(m+1\right)x+m^2+3m-1=0\)
\(\Delta=b^2-4ac=\left[-2\left(m+1\right)\right]^2-4\left(m^2+3m-1\right)\)
\(=4\left(m^2+2m+1\right)-4\left(m^2+3m-1\right)\)
\(=4m^2+8m+4-4m^2-12m+4\)
\(=-4m+8\)
Để pt có 2 nghiệm \(x_1,x_2\) thì \(\Delta>0\Leftrightarrow-4m+8>0\Leftrightarrow-4m>-8\Leftrightarrow m< 2\)
Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m+1\right)=2m+2\\x_1x_2=\dfrac{c}{a}=m^2+3m-1\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-10=0\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(m^2+3m-1\right)-10=0\)
\(\Leftrightarrow4m^2+8m+4-2m^2-6m+2-10=0\)
\(\Leftrightarrow2m^2+2m-4=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\left(tmdk\right)\\m=-2\left(tmdk\right)\end{matrix}\right.\)
Vậy \(m=1,m=-2\) thì thỏa mãn đề bài.
3:
a: 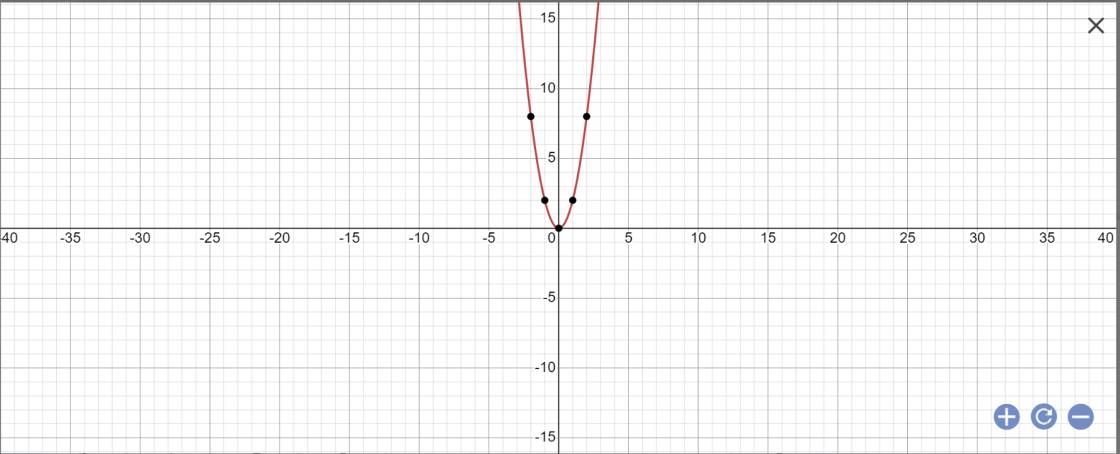
b: Δ=(2m+2)^2-4(m^2+3m-1)
=4m^2+8m+4-4m^2-12m+4=-4m+8
Để pt có hai nghiệm pb thì -4m+8>0
=>m<2
x1^2+x2^2=10
=>(x1+x2)^2-2x1x2=10
=>4m^2+8m+4-2m^2-6m+2=10
=>2m^2+2m-4=0
=>m^2+m-2=0
=>m=-2 hoặc m=1
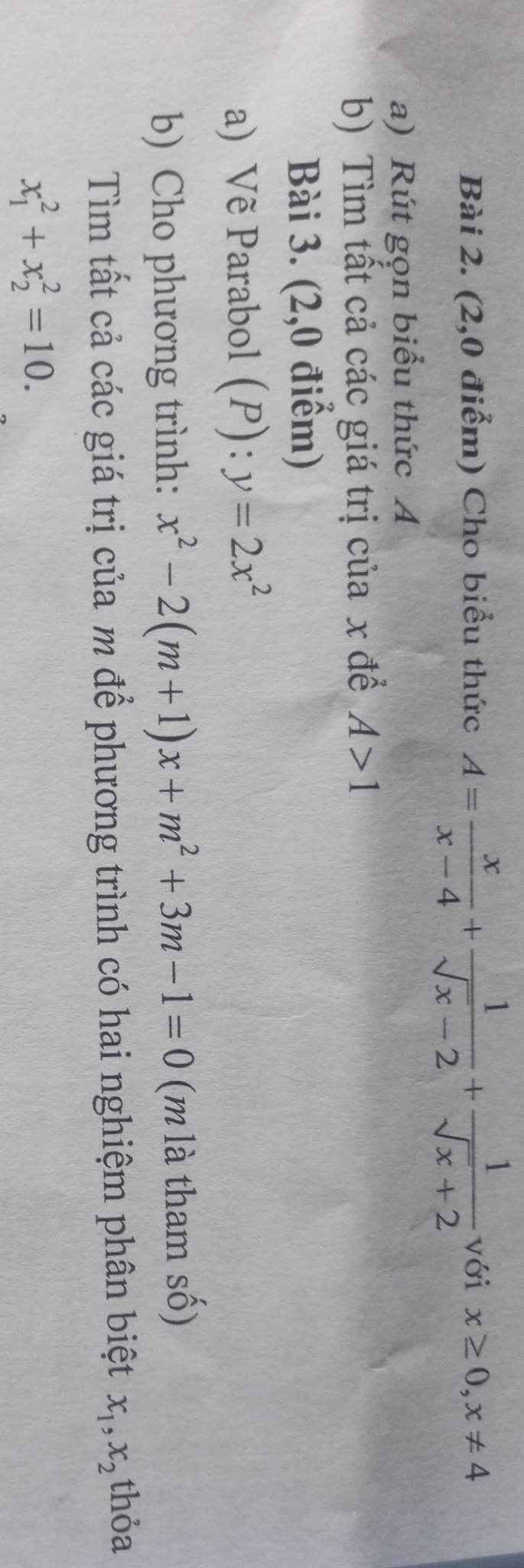




 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ



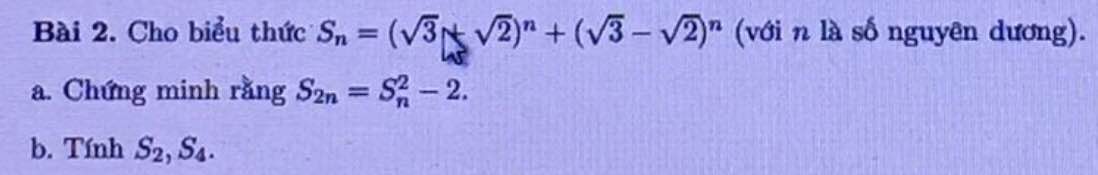 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺