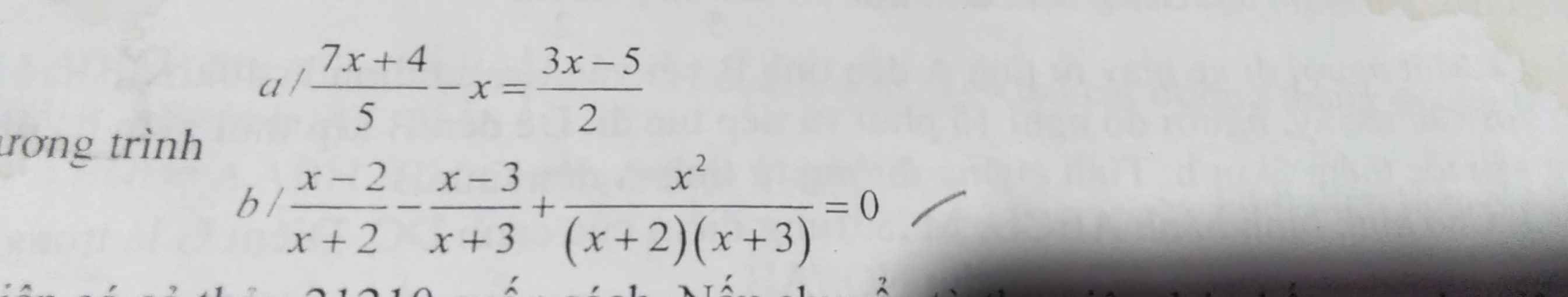a) Ta có: \(\dfrac{7x+4}{5}-x=\dfrac{3x-5}{2}\)
\(\Leftrightarrow\dfrac{2\left(7x+4\right)}{10}-\dfrac{10x}{10}=\dfrac{5\left(3x-5\right)}{10}\)
Suy ra: \(14x+8-10x=15x-25\)
\(\Leftrightarrow4x+8-15x+25=0\)
\(\Leftrightarrow-11x+33=0\)
\(\Leftrightarrow-11x=-33\)
hay x=3
Vậy: S={3}
b) ĐKXĐ: \(x\notin\left\{-2;-3\right\}\)
Ta có: \(\dfrac{x-2}{x+2}-\dfrac{x-3}{x+3}+\dfrac{x^2}{\left(x+2\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x+3\right)}{\left(x+2\right)\left(x+3\right)}-\dfrac{\left(x-3\right)\left(x+2\right)}{\left(x+3\right)\left(x+2\right)}+\dfrac{x^2}{\left(x+2\right)\left(x+3\right)}=0\)
Suy ra: \(x^2+3x-2x-6-\left(x^2+2x-3x-6\right)+x^2=0\)
\(\Leftrightarrow2x^2+x-6-x^2+x+6=0\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
Vậy: S={0}