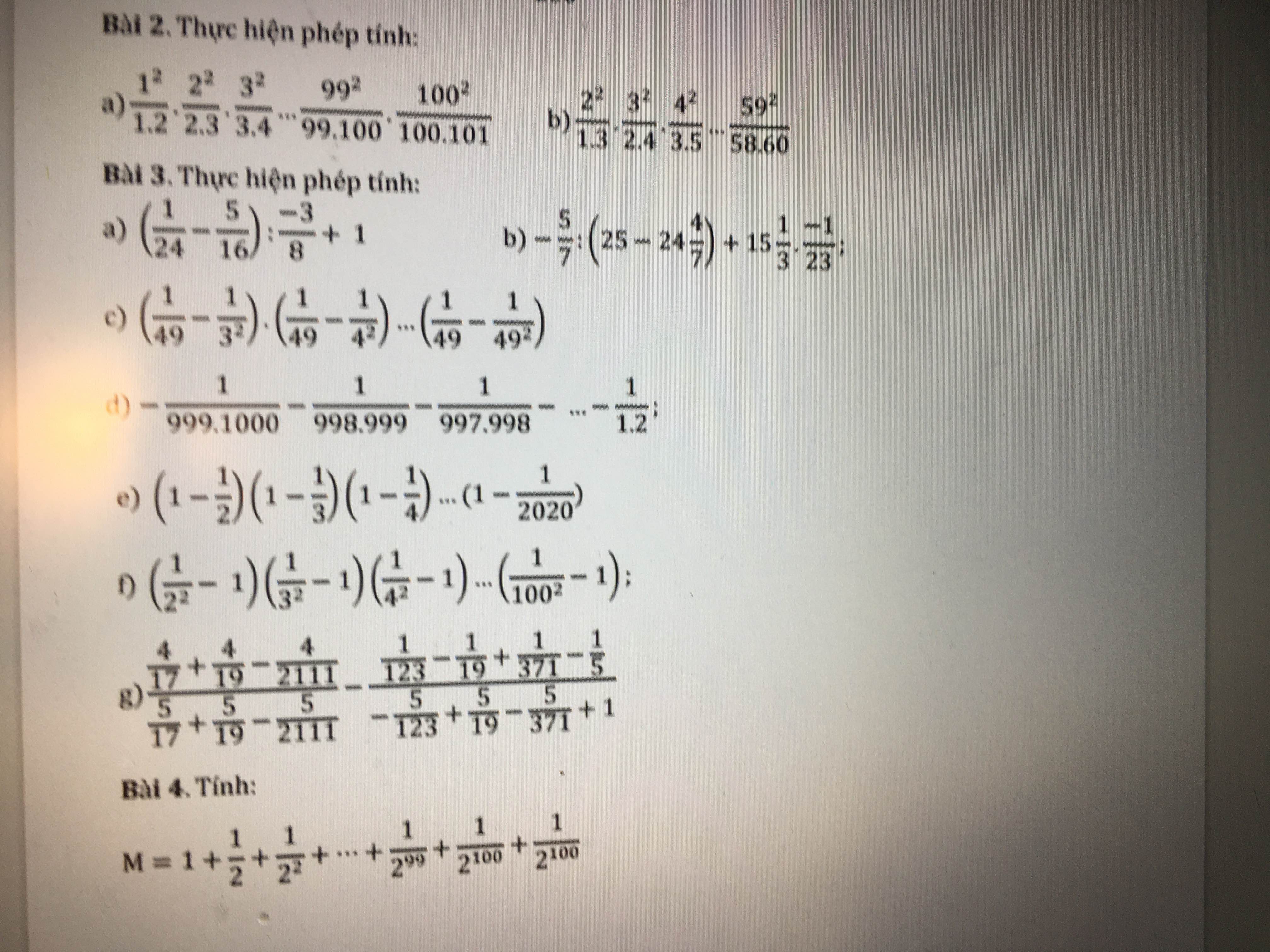4:
\(M=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}+\dfrac{1}{2^{99}}\)
\(=1+\dfrac{1}{2}+...+\dfrac{1}{2^{98}}+\dfrac{2}{2^{99}}\)
=...
=2
3:
a: \(=\left(\dfrac{2}{48}-\dfrac{15}{48}\right)\cdot\dfrac{-8}{3}+1\)
=13/48*8/3+1
=13/18+1=31/18
b: \(=\dfrac{-5}{7}:\left(1-\dfrac{4}{7}\right)+\dfrac{46}{3}\cdot\dfrac{-1}{23}\)
=-5/7:3/7+-2/3
=-2/3-5/3=-7/3
c: =A*(1/49-1/7^2)=0
e: =1/2*2/3*...*2019/2020=1/2020