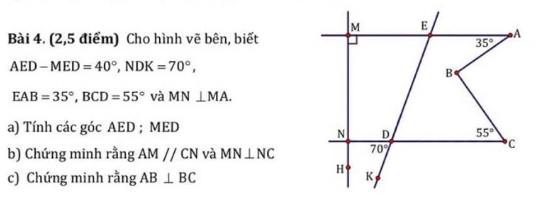
a: Ta có: \(\widehat{AED}-\widehat{MED}=40^0\)
\(\widehat{AED}+\widehat{MED}=180^0\)(hai góc kề bù)
Do đó: \(\widehat{AED}=\dfrac{40^0+180^0}{2}=110^0;\widehat{MED}=180^0-110^0=70^0\)
b: ta có: \(\widehat{MED}=\widehat{NDK}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên AM//CN
ta có: AM//CN
AM\(\perp\)MN
Do đó: CN\(\perp\)MN
c: Qua B, kẻ tia BF nằm giữa hai tia BA và BC sao cho BF//AM//CN
ta có: BF//AM
=>\(\widehat{FBA}=\widehat{BAE}\)(hai góc so le trong)
=>\(\widehat{FBA}=35^0\)
Ta có: BF//CN
=>\(\widehat{FBC}=\widehat{BCD}\)(hai góc so le trong)
=>\(\widehat{FBC}=55^0\)
\(\widehat{ABC}=\widehat{ABF}+\widehat{CBD}=35^0+55^0=90^0\)
=>BA\(\perp\)BC
Đúng 1
Bình luận (0)
