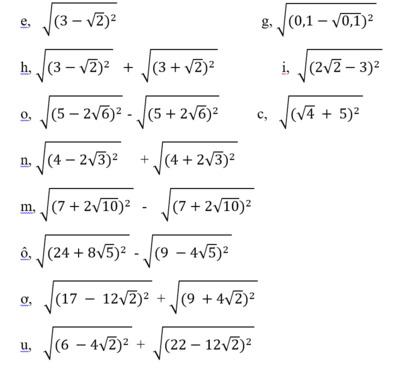a, Theo tc 2 tt cắt nhau: \(AE=EC;BF=CF\)
Vậy \(AE+BF=EC+CF=EF\)
b, Vì \(\left\{{}\begin{matrix}AE=EC\\\widehat{EAO}=\widehat{ECO}=90^0\\OE.chung\end{matrix}\right.\) nên \(\Delta AOE=\Delta COE\)
\(\Rightarrow\widehat{AOE}=\widehat{EOC}\) hay OE là p/g \(\widehat{AOC}\)
Cmtt: \(\Delta BOF=\Delta COF\Rightarrow\widehat{BOF}=\widehat{COF}\) hay OF là p/g \(\widehat{BOC}\)
Vậy \(\widehat{EOF}=\widehat{COF}+\widehat{COE}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{BOC}\right)=90^0\) hay OE⊥OF




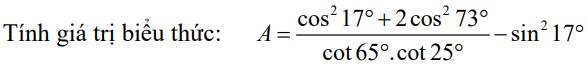


 giúp mik vs mng ơi.mik cần gấp á
giúp mik vs mng ơi.mik cần gấp á