c: \(\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{6}\right|+...+\left|x+\dfrac{1}{110}\right|=11x\)
mà \(\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{6}\right|+...+\left|x+\dfrac{1}{110}\right|>=0\)
nên 11x>=0
=>x>=0
Phương trình sẽ trở thành:
\(x+\dfrac{1}{2}+x+\dfrac{1}{6}+...+x+\dfrac{1}{110}=11x\)
=>\(x+\dfrac{1}{1\cdot2}+x+\dfrac{1}{2\cdot3}+...+x+\dfrac{1}{10\cdot11}=11x\)
=>\(11x=10x+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
=>\(11x=10x+1-\dfrac{1}{11}=10x+\dfrac{10}{11}\)
=>\(x=\dfrac{10}{11}\left(nhận\right)\)
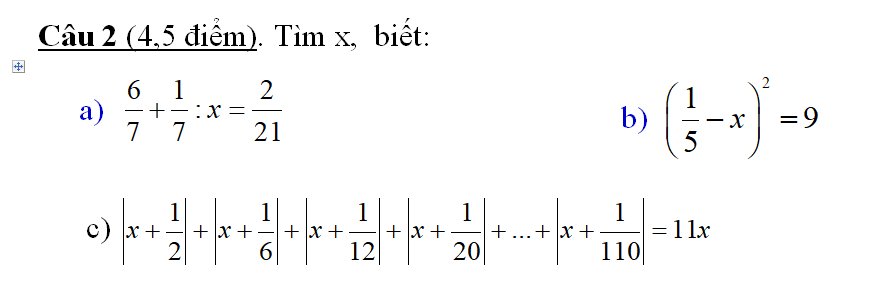


 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 
 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ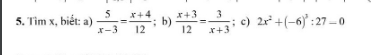

 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ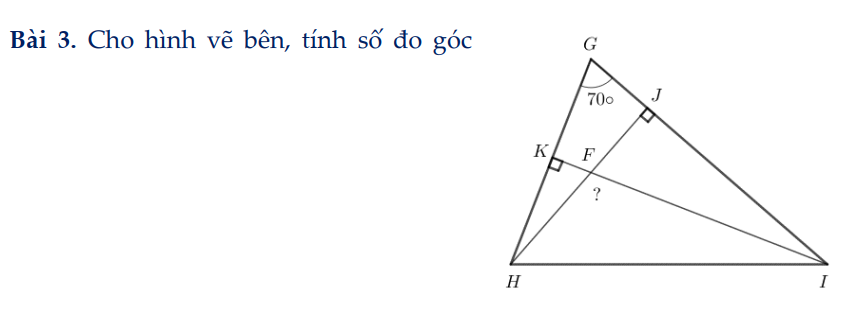 cần gấp
cần gấp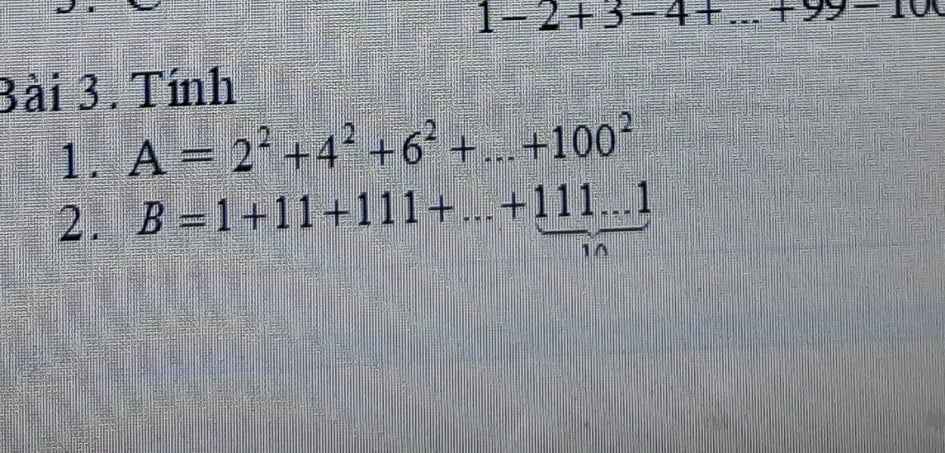 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn