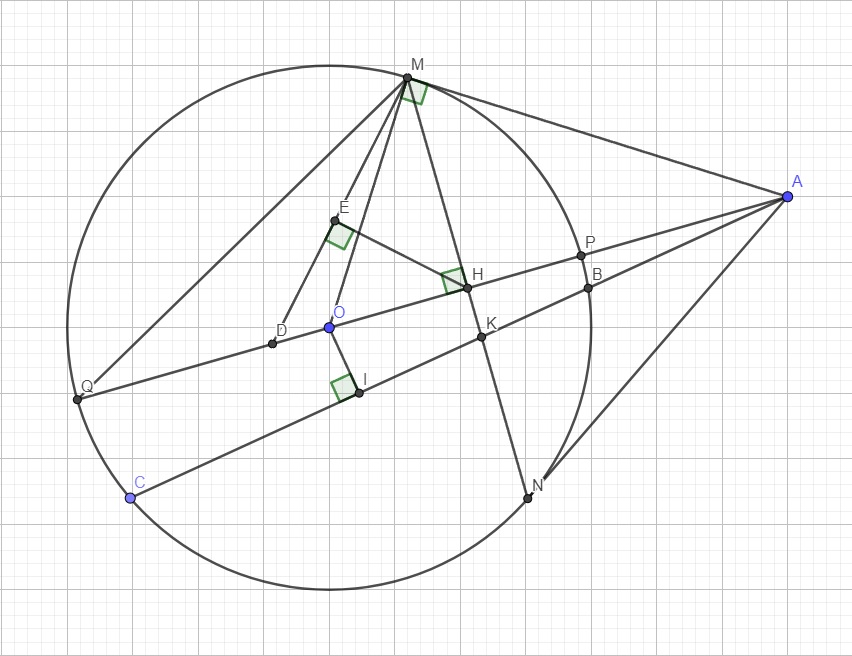
a.
Do AM là tiếp tuyến \(\Rightarrow AM\perp OM\Rightarrow\widehat{AMO}=90^0\)
AN là tiếp tuyến \(\Rightarrow AN\perp ON\Rightarrow\widehat{ANO}=90^0\)
\(\Rightarrow M,N\) cùng nhìn AO dưới 1 góc vuông nên tứ giác AMON nội tiếp
b.
Ta có: \(\left\{{}\begin{matrix}AM=AN\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\\OM=ON=R\end{matrix}\right.\)
\(\Rightarrow OA\) là trung trực MN
\(\Rightarrow OA\perp MN\) tại H
Áp dụng hệ thức lượng trong tam giác vuông AOM với đường cao MH:
\(AM^2=AH.AO\) (1)
Do I là trung điểm BC \(\Rightarrow OI\perp BC\Rightarrow\widehat{OIA}=90^0\)
Xét hai tam giác vuông OIA và KHA có:
\(\left\{{}\begin{matrix}\widehat{OIA}=\widehat{KHA}=90^0\\\widehat{OAI}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OIA\sim\Delta KHA\left(g.g\right)\)
\(\Rightarrow\dfrac{AO}{AK}=\dfrac{AI}{AH}\Rightarrow AH.AO=AK.AI\) (2)
(1);(2) \(\Rightarrow AK.AI=AM^2\)
c.
Câu này rõ ràng đề sai. Nhìn hình là thấy liền. Tam giác MHE vuông còn tam giác QDM không vuông nên chúng ko thể đồng dạng. Và P thì ko thể là trung điểm ME rồi.